3.3: Oscillation of a Dipole in an Electric Field

Consider a dipole oscillating in an electric field (Figure III.3). When it is at an angle $\theta$ to the field, the magnitude of the restoring torque on it is $pE \sin \theta$, and therefore its equation of motion is

$$I\ddot \theta = -pE\sin \theta \label{1}$$

where $I$ is its rotational inertia.

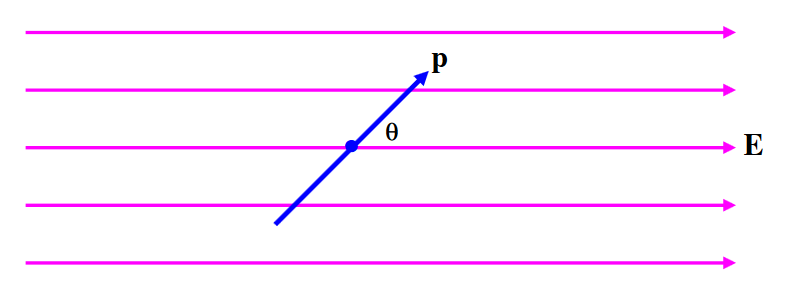
$\text{FIGURE III.3}$

For small angles, Equation $\ref{1}$ can be approximated as

$$I\ddot \theta \approx -pE\theta$$

and so the period of small oscillations is

$$\label{3.3.1}P=2\pi\sqrt{\frac{I}{pE}}.$$

Would you expect the period to be long if the rotational inertia were large? Would you expect the vibrations to be rapid if $p \text{ and }E$ were large? Is the above expression dimensionally correct?