17.3: The Elements of the True Orbit

Unless we are dealing with photographic measurements in which we have been able to measure the positions of both components with respect to their mutual centre of mass, I shall assume that we are determining the orbit of the secondary component with respect to the primary as origin and focus.

\(\text{FIGURE XVII.2}\)

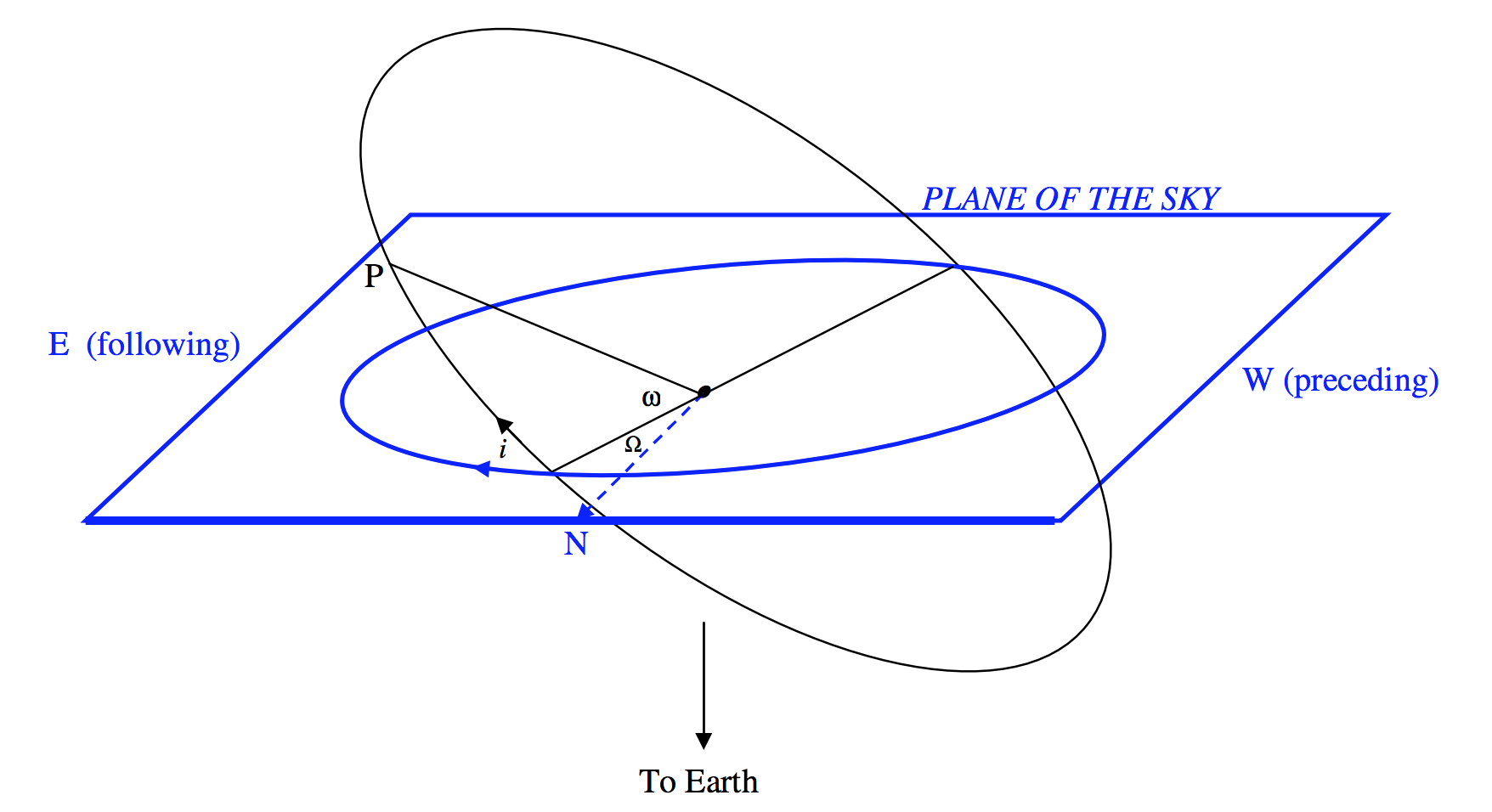
In figure \(\text{XVII.2}\), which has tested my artistic talents and computer skills to the full, the blue plane is intended to represent the plane of the sky, as seen from “above” – i.e. from outside the celestial sphere. Embedded in the plane of the sky is the apparent orbit of the secondary with respect to the primary as origin and focus. The dashed arrow shows the colure (definition of “colure” – Section 6.4 of Chapter 6) through the primary, and points to the north celestial pole. The primary star is not necessarily at a focus of the apparent ellipse, as discussed in the previous section. As drawn, the position angle of the star is increasing with time – though of course in a real case it is equally likely to be increasing or decreasing with time.

The black ellipse is the true orbit, and of course the primary is at a focus of it. If it does not appear so in figure \(\text{XVII.2}\), this is because the true orbit is being seen in projection.

The elements of the true orbit to be determined (if possible) are

• \(a\) the semi major axis;
• \(e\) the eccentricity;
• \(i\) the inclination of the plane of the orbit to the plane of the sky;
• \(Ω\) the position angle of the ascending node;
• \(ω\) the argument of periastron;
• \(T\) the epoch of periastron passage.

All of these will be familiar to those who have read Chapter 10, section 10.2. Some comments are necessary in the context of the orbit of a visual binary star.

Ideally, the semi major axis would be expressed in kilometres or in astronomical units of distance – but this is not possible unless the distance from Earth to the binary star is known. If the distance is not known (as will often be the case), the semi major axis is customarily expressed in arcseconds.

It is sometimes said that, from measurements of separation and position angle alone, and with no further information, and in particular with no spectroscopic measurements of radial velocity, it is not possible to determine the sign of the inclination of the true orbit of a visual binary star. This may be a valid view, but, as the late Professor Joad might have said, it all depends on what you mean by “inclination”. As with the orbits of planets around the Sun, as described in Chapter 10, Section 10.2, we take the point of view here that the inclination of the orbital plane to the plane of the sky is an angle that lies between \(0^\circ\) and \(180^\circ\) inclusive; that is to say, the inclination is positive, and the question of its sign does not arise. After all an inclination of, say, “\(−30^\circ\)” is no different from an inclination of \(+150^\circ\). Thus we cannot be ignorant of the “sign” of the inclination. What we do not know, however, is which node is the ascending node and which is the descending node.

The \(Ω\) that is usually recorded in the analysis of the orbit of a visual binary unsupported by spectroscopic radial velocities is the node for which the position angle is less than \(180^\circ\) – and it is not known whether this is the ascending or descending node.

If the inclination of the orbital plane is less than \(90^\circ\), the position angle of the secondary will increase with time, and the orbit is described as direct or prograde. If the position angle decreases with time, the orbit is retrograde.

The orbital inclination of a spectroscopic binary cannot be determined from spectroscopic observations alone. The inclination of a visual binary can be determined, although, as discussed above, it is not known which node is ascending and which is descending. If the binary is both a visual binary and a spectroscopic binary, not only can the inclination be determined, but the ambiguity in the nodes is removed. In addition, it may be possible to determine the masses of the stars; this aspect will be dealt with in the chapter on spectroscopic binary stars.

Binary stars that are simultaneously visual and spectroscopic binaries are rare, and they are a copious source of valuable information when they are found. Visual binary stars, unless they are relatively close to Earth, have a large true separation, and consequently their orbital speeds are usually too small to be measured spectroscopically. Spectroscopic binary stars, on the other hand, move fast in their orbits, and this is because they are close together – usually too close to be detected as visual binaries. Binaries that are both visual and spectroscopic are usually necessarily relatively close to Earth.

The element \(ω\), the argument of periastron, is measured from the ascending node (or the first node, if, as is usually the case, the type of node is unknown) from \(0^\circ\) to \(360^\circ\) in the direction of motion of the secondary component.