6.9: The Length of the Year
- Page ID
- 8169
The time taken for Earth to revolve around the Sun with respect to the stars, which is the same thing as the time taken for the Apparent Sun to move around the ecliptic with respect to the stars, is a Sidereal Year, which is \(365^{\text{d}} .25636\), where the “d” denotes a mean solar day. The length of the seasons, however, is determined by the motion of the Apparent Sun relative to \(\Upsilon\). Because \(\Upsilon\) is moving westward along the ecliptic, the time that the Apparent Sun takes to move around the ecliptic relative to \(\Upsilon\), which is called the Tropical Year, is a little less than the sidereal year. We have seen, however that the motion of \(\Upsilon\) along the ecliptic is not quite uniform, and we have to average out the effects of nutation. Thus the Mean Tropical Year is the average time for the ecliptic longitude of the Apparent Sun to increase by \(360^\circ\), which is \(365^\text{d} .24219\).
The calendar that we use in everyday life is the Gregorian Calendar, in which there are 365 days in most years, but 366 days in years that are divisible by 4 unless they are also divisible by 100 other than those that are also divisible by 400. Thus leap years (those that have 366 days) include 1996, 2000, 2004, but not 2005 or 1900. (2000 was a leap year because, although it is divisible by 100, it is also divisible by 400.) The average length of the Gregorian Year is 365.2425, which is close enough to the Mean Tropical Year for present-day purposes, but which is of concern to calendar reformers and will be of some concern to our remote descendants.
The Anomalistic Year is the interval between consecutive passages of the Earth through perihelion. The perihelion of Earth’s orbit is slowly advancing in the same direction as the Earth’s motion, so the anomalistic year is a little longer than the sidereal year, and is equal to \(365^\text{d} .25964\).
Figure \(\text{VI.9}\) illustrates a way of thinking about the relation between the sidereal and tropical years. We are looking down on the ecliptic from the direction of the north ecliptic pole. We see the Sun moving counterclockwise at angular speed \(ω_\text{sid}\) and moving clockwise at angular speed \(ω_\Upsilon\). The angular speed of the Sun relative to \(\Upsilon\)
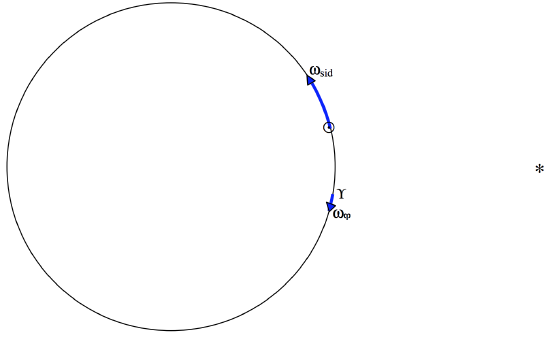
\(\text{FIGURE VI.9}\)
is \(ω_\text{trop} = ω_\text{sid} + ω_\Upsilon\). But period \(P\) and angular speed \(ω\) are related by \(ω = 2π/P\).
Therefore: \[\frac{1}{P_\text{trop}} = \frac{1}{P_\text{sid}} + \frac{1}{P_\Upsilon}. \label{6.9.1} \tag{6.9.1}\]
Thus \(P_\text{sid} = 365^\text{d} .25636\) and \(P_\Upsilon = 25800 \ \text{years} = 9.424 \times 10^6 \ \text{days}\). Hence \(P_\text{trop} = 365^\text{d} .2422\). Using the same argument, see if you can calculate how long it takes for the perihelion of Earth’s orbit to advance by \(360^\circ\) – bearing in mind that the perihelion is advancing, not regressing.
One more point worth noting is that, during a sidereal year, the Sun has upper transited across the meridian 365.25636 times, whereas a fixed star has transited 366.25636 times. Expressed another way, while Earth turns on its axis 365.25636 times relative to the Sun, relative to the stars it has made one extra turn during its revolution around the Sun. Thus
\[\frac{\text{Length of sidereal day}}{\text{Length of solar day}} = \frac{365.25636}{366.25636}. \]
Thus the length of the sidereal day is \(23^\text{h} \ 56^\text{m} \ 04^\text{s}\).


