13.3: Sectors

Last updated
Save as PDF

Page ID: 6870

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Figure XIII.2 shows a portion of an elliptic (or other conic section) orbit, and it shows the radii vectores of the planet’s position at instants of time \(t_1, \ t_2\) and \(t_3\).

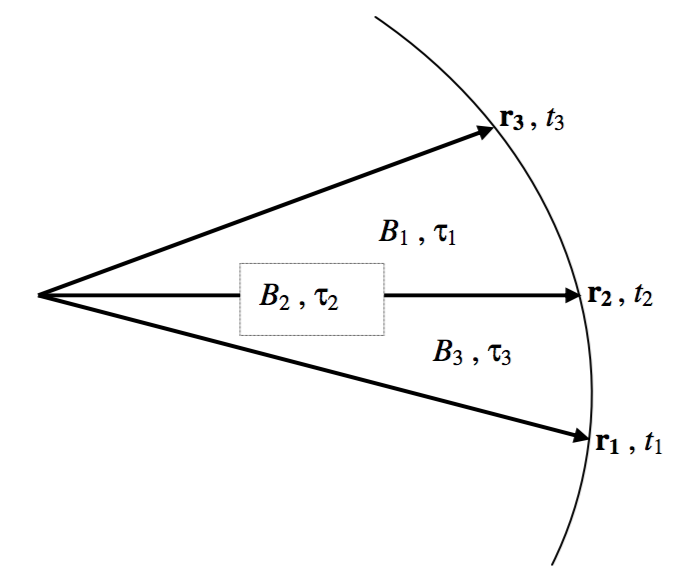
Figure 13.2.png
\(\text{FIGURE XIII.2}\)

The notation I am going to use is as follows:

The area of the sector formed by joining the tips of \(\textbf{r}_2\) and \(\textbf{r}_3\) around the orbit is \(B_1\).
The area of the sector formed by joining the tips of \(\textbf{r}_3\) and \(\textbf{r}_1\) around the orbit is \(B_2\).
The area of the sector formed by joining the tips of \(\textbf{r}_1\) and \(\textbf{r}_2\) around the orbit is \(B_3\).

The time interval \(t_3 − t_2\) is \(τ_1\).
The time interval \(t_3 − t_1\) is \(τ_2\).
The time interval \(t_2 − t_1\) is \(τ_3\).

Provided the arc is fairly small, then to a good approximation (in other words we can approximate the sectors by triangles), we have

\[B_2 \textbf{r}_2 \approx B_1 \textbf{r}_1 + B_3 \textbf{r}_3 . \label{13.3.1} \]

That is,

\[\textbf{r}_2 \approx b_1 \textbf{r}_1 + b_3 \textbf{r}_3 , \label{13.3.2} \]

where

\[b_1 = B_1/B_2 \label{13.3.3} \]

and

\[b_3 = B_3 / B_2 \label{13.3.4} \]

The coefficients \(b_1\) and \(b_3\) are the sector ratios, and the coefficients \(a_1\) and \(a_3\) are the triangle ratios.

By Kepler’s second law, the sector areas are proportional to the time intervals.

That is \[b_1 = τ_1 / τ_2 \label{13.3.5} \]

and \[b_3 = τ_3 / τ_2 . \label{13.3.6} \]

Thus the coefficients in Equation \ref{13.3.2} are known. Our aim is to use this approximate Equation to find approximate values for the heliocentric distances at the instants of the three observations, and then to refine them in order to satisfy the exact Equation 13.2.5. We shall embark upon our attempt to do this in Section 13.6, but we should first look at the following three sections.