3.1: A Brief History of the Lommel-Seeliger Law
- Page ID
- 7503
Introduction. The use of the Lommel-Seeliger law is an enduring aspect of planetary photometry. It has the advantage of analytical simplicity as well as, in many cases, being an excellent first approximation to diffuse reflection. In spite of its shortcomings, in particular its inability to display an opposition effect, it is still very much in use today in applications as diverse as lightcurve inversion (the determination of asteroid poles and shapes from their lightcurves (Kaasalainen, 2003)), to the prediction of photometric signatures of unresolved ringed extrasolar planets (Arnold & Schneider, 2004). Indeed, it is the topic of exoplanets which has recently generated an interest in planetary photometry by astronomers who would otherwise not be concerned with the subject.
Here we present the Lommel-Seeliger law in some detail and as a result point out the existence and consequences of an insidious error, which has percolated down through the literature.
Description. The Lommel-Seeliger law is based on a simple physical model of diffuse reflection. As such it is a single scattering model in which the scattering is isotropic.
The model assumes that light penetrates the surface, being attenuated exponentially as it does so. Here attenuation refers to any process which reduces the brightness of a beam of light, and thus includes scattering and absorption. Each element of volume encountered by the attenuated beam scatters part of it isotropically, i.e. equally in all directions into the \(4π\) steradians (the imaginary sphere, if you like) surrounding it. Thus, of this diffuse scattered radiation, only half is directed back towards the surface, and this fraction will be further attenuated before emerging as diffuse reflected radiation.
Derivation. The following derivation is intended to be more illustrative than entirely rigorous and contains a few shortcuts. It is nonetheless correct; for a more robust and general proof see Chapter 1.
Consider, as shown in Figure \(\PageIndex{1}\), a diffuse reflecting (and transmitting) layer of normal optical thickness \(t\), in which the optical thickness includes attenuation by both scattering and absorption. In problems of this nature, it is more convenient to work in terms of optical thickness than actual physical thickness. Light traversing a path of optical thickness \(τ\) is attenuated by a factor \(e^{-τ}\).
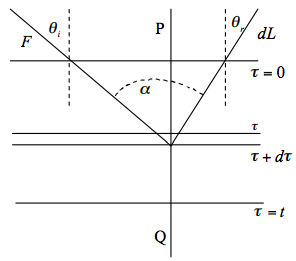
The surface (τ = 0) is irradiated by a plane parallel beam of radiant flux density \(F\) at an angle of incidence \(θ_i\), so that the irradiance is \(E = F \cos θ)i\). We are concerned with the resulting radiance in the direction of an angle of reflection \(θ_r < 90^o\). Now let \(μ_0 = \cos θ_i\) and \(μ = \cos θ_r\) and consider the layer between \(τ\) and \(τ + dτ\). The incident flux density which has penetrated to this level is \(Fe^{-τ/μ_0}\).
The contribution to the diffuse radiance in the direction μ by isotropic scattering is thus \( \dfrac{\varpi_{0}}{4 \pi} F e^{-\tau / \mu_{0}} \dfrac{d \tau}{\mu}\) where \(ϖ_0\) is the single scattering albedo. This radiation will be further attenuated by the factor \(e^{-τ/μ}\) before emerging from the surface, so that the contribution to the radiance in the direction \(μ\) is
\[d L=\dfrac{\varpi_{0}}{4 \pi} F e^{-\tau / \mu_{0}} \dfrac{d \tau}{\mu} e^{-\tau / \mu}.\]
Note that \(dL\) is the contribution to the total radiance from the layer resulting from single scattering. The Lommel-Seeliger model considers only the scattering of the collimated incident light. It does not take into account scattering of diffuse light which has made its way indirectly to the same position by being scattered one or more times, i.e. it does not consider multiple scattering.
For a planetary surface, the layer is “semi-infinite” (\(t = ∞\)) and the total radiance in the direction \(μ\) is
\[L=\dfrac{\varpi_{0} F}{4 \pi \mu} \times \int_{0}^{\infty} \exp \left[-\tau\left(\dfrac{1}{\mu_{0}}+\dfrac{1}{\mu}\right)\right] d \tau.\]
resulting in
\[L=\dfrac{\varpi_{0} F}{4 \pi \mu} \dfrac{\mu_{0} \mu}{\mu+\mu_{0}};\]
and, since the irradiance is \(E = Fμ_0\) and \(L = f_r E\), it follows that the bidirectional reflectance distribution function (BRDF) which defines the Lommel -Seeliger reflectance rule is
\[f_{r}=\dfrac{\varpi_{0}}{4 \pi} \dfrac{1}{\mu+\mu_{0}}.\]
The use of the Lommel-Seeliger model is not restricted to planetary surfaces. For a layer of finite optical thickness t, e.g. an (exo)planetary ring, the reflected radiance is
\[L_{R}=\dfrac{\varpi_{0} F}{4 \pi \mu} \times \int_{0}^{t} \exp \left[-\tau\left(\dfrac{1}{\mu_{0}}+\dfrac{1}{\mu}\right)\right] d \tau,\]
resulting in
\[L_{R}=\dfrac{\varpi_{0}}{4 \pi} \dfrac{1}{\mu+\mu_{0}} \times\left[1-\exp \left\{-t\left(\dfrac{1}{\mu_{0}}+\dfrac{1}{\mu}\right)\right\}\right] \mu_{0} F;\]
and by similar reasoning the radiance \(L_T\) transmitted through the layer may be determined (Arnold & Schneider, 2004).
Errors in the Literature. The oldest error which the author has been able to detect dates back to 1916 in a paper on planetary albedos by (no less than) Henry Norris Russell (Russell, 1916). In that paper the BRDF is implicitly expressed as
\[f_{r}=\dfrac{\gamma}{\mu_{0}+\mu}\]
in which \(γ\) is a constant. From this Russell derives the directional hemispherical reflectance (hemispherical albedo)
\[\rho\left(\mu_{0}\right)=2 \pi \gamma \quad \times \quad\left[1-\mu_{0} \ln \left(1+1 / \mu_{0}\right)\right],\]
where it may be seen that the expression in brackets varies monotonically from 0.308 (μ0 = 1) to unity (μ0 = 0); he then argues “ Since (ρ) can never exceed unity it follows that πγ cannot be greater 0.5 nor (the Bond albedo) A than 0.409. Hence a planet for which (the geometrical albedo) p exceeds 0.25 cannot reflect light in strict accordance with the Lommel-Seeliger law”.
Although this argument sounds entirely plausible, it is wrong. While it is true that \(ρ\), like any albedo, cannot exceed unity, in the case of the Lommel-Seeliger law it cannot exceed \( \dfrac{1}{2}\) and therefore the maximum value of γ is \( \dfrac{1}{4 \pi}\) not \( \dfrac{1}{2 \pi}\); the value of γ is \( \dfrac{\varpi_{0}}{4 \pi}\). Such an error can affect albedo calculations by a fact or of two. Unfortunately, this error has filtered down into subsequent publications, e.g. Lester, McCall & Tatum (1979), Fairbairn (2002, 2004). The correct properties of the LommelSeeliger law are summarised in Table I.
| Properties of Surfaces | the Lommel-Seeliger Reflectance Law | Spheres | |
|---|---|---|---|
| fr | \(\dfrac{\varpi_{0}}{4 \pi} \dfrac{1}{\mu_{0}+\mu}\) | q | \(\dfrac{16}{3}(1-\ln 2)\) |
| ρ (0.5) | \(\dfrac{\varpi_{0}}{2}\left[1-\mu_{0} \ln \left(1+1 / \mu_{0}\right)\right]\) | p (0.125) | \( \dfrac{ \varpi_0}{8}\) |
| pn (0.125) | \( \dfrac{ \varpi_0}{8}\) | A (0.2046) | \(\dfrac{2}{3} \varpi_{0}(1-\ln 2)\) |
For some applications, the error of a factor of two is of no consequence. In cases where only relative magnitudes matter, so that the offset is arbitrary, the factor disappears into the offset. Asteroid lightcurve profiles are such examples.
References
Arnold, L. & Schneider, J. 2004, A&A, 420, 1153-1162
Fairbairn, M. B. 2002, JRASC, 96, 18
Fairbairn, M. B. 2004, JRASC, 98, 149
Hapke, B. 1981, J. Geophys. Res., 86, 3039
Kaasalainen, M. 2003, JRASC, 97, 283
Lester, P.L., McCall, M.L. & Tatum, J.B. 1979, JRASC, 73, 233
Russell, H.N. 1916, ApJ, 43, 173


