6.3: Equatorial Coordinates
- Page ID
- 6821
If you live in the northern hemisphere and if you face north, you will observe that the entire celestial sphere is rotating slowly counterclockwise about a point in the sky close to the star Polaris (\(α\) Ursae Minoris). The point \(\text{P}\) about which the sky appears to rotate is the North Celestial Pole. If you live in the southern hemisphere and if you face south you will see the entire sky rotating clockwise about a point \(\text{Q}\), the South Celestial Pole. There is no bright star near the south celestial pole; the star \(σ\) Octantis is close to the south celestial pole, but it is only just visible to the unaided eye provided you are dark adapted and if you have a clear sky free of light pollution. The great circle that is \(90^\circ\) from either pole is the celestial equator, and it is the projection of Earth’s equator on to the celestial sphere.
\(\text{FIGURE VI.2}\)
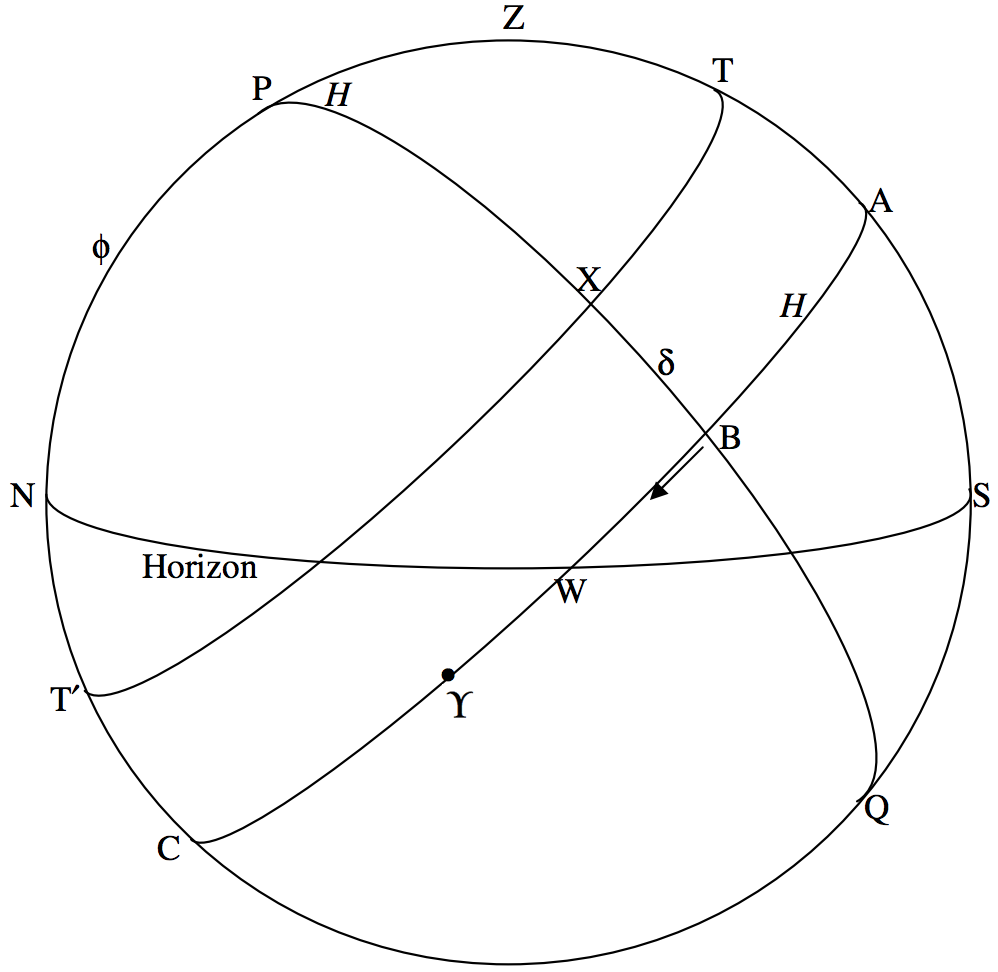
In figure \(\text{VI.2}\) I have drawn the celestial sphere from the opposite side from the drawing of figure \(\text{VI.1}\), so that, this time, you can see the west point of the horizon, but not the east point. The celestial equator is the great circle \(\text{ABW} \Upsilon \text{C}\).
You might possibly have noticed that, in section 2, I had not properly defined the north point of the horizon other than by saying that it was the point marked \(\text{N}\) in figure VI.1. We see now that the north and south points of the horizon are the points where the vertical circle that passes through the celestial poles (i.e. the meridian) meets the horizon.
The altitude \(\phi\) of the north celestial pole is equal to the geographical north latitude of the observer. Thus for an observer at Earth’s north pole, the north celestial pole is at the zenith, and for an observer at Earth’s equator, the north celestial pole is on the horizon.
You will see that a star such as \(\text{X}\) transits across the meridian twice. Lower meridian transit occurs at the point \(\text{T}^\prime\), when the star is north of the observer and is directly below the north celestial pole. For the star \(\text{X}\) of figure \(\text{VI.2}\), lower meridian transit is also below the horizon, and it cannot be seen. The star reaches its highest point in the sky (i.e. it culminates) at upper meridian transit.
The first quantitative astronomical observation I ever did was to see how long the celestial sphere takes to rotate through \(360^\circ\). This is best done by timing the interval between two consecutive upper meridian transits of a star. It will be found that this interval is \(23^{\text{h}} \ 56^{\text{m}} \ 04^{\text{s}} .099\) of mean solar time, although of course it requires more than a casual observation to determine the interval to that precision. The rotation of the celestial sphere is, of course, a reflection of the rotation of Earth on its axis. In other words, this interval is the sidereal (i.e. relative to the stars) rotation period of Earth.
We are now in a position to describe the position of a star on the celestial sphere in equatorial coordinates. The angle \(δ\) in figure \(\text{VI.2}\) is called the declination of the star. It is usually expressed in degrees, arcminutes and arcseconds, from \(0^\circ\) to \(+90^\circ\) for stars on or north of the equator, and from \(0^\circ\) to \(−90^\circ\) for stars on or south of the equator. When quoting the declination of a star, the sign of the declination must always be given.
When the star \(\text{X}\) in figure \(\text{VI.2}\) is at lower meridian transit, it is below the horizon and is not visible. However, if the declination of a star is greater than \(90^\circ − \phi\), the star will not reach the horizon and it will never set. Such stars are called circumpolar stars.
The second coordinate is the angle \(H\) in figure \(\text{VI.2}\). It is measured westward from the meridian. It will immediately be noticed that, while the declination of a star does not change through the night, its hour angle continuously increases, and also the hour angle of a star at any given time depends on the geographical longitude of the observer. While hour angle could be expressed in either radians or degrees, it is customary to express the hour angle in hours, minutes and seconds of time. Thus hour angle goes from \(0^{\text{h}}\) to \(24^{\text{h}}\). When a star has an hour angle of, for example, \(3^{\text{h}}\), it means that it is three sidereal hours since it transited (upper transit) the meridian. Conversion factors are
\[1^{\text{h}} = 15^\circ \quad 1^{\text{m}} = 15^\prime \quad 1^{\text{s}} = 15^{\prime \prime} \quad 1^\circ = 4^{\text{m}} \quad 1^\prime = 4^{\text{s}}.\]
(The reader may have noticed that I have just used the term “sidereal hours”. For the moment, just read this as “hours” – but a little later on we shall say what we mean by “sidereal” hours, and you may then want to come back and re-read this.)
While it is useful to know the hour angle of a star at a particular time for a particular observer, we still need a coordinate that is fixed on the celestial sphere. To do this, we refer to a point on the celestial equator, which I shall define more precisely later on, denoted on figure \(\text{VI.2}\) by the symbol \(\Upsilon\). This is the astrological symbol for the sign Aries, and it was originally in the constellation Aries, although at the present time it is in the constellation Pisces. In spite of its present location, it is still called the First Point of Aries. The angle measured eastward from \(\Upsilon\) to the point \(\text{B}\) is called the right ascension of the star \(\text{X}\), and is denoted by the symbol \(α\). This does not change (at least not very much – but we shall deal with small refinements later) during the night or from night to night. Thus we can describe the position of a star on the celestial sphere by the two coordinates \(δ\), its declination, and \(α\), its right ascension, and since its right ascension does not change (at least not very much), we can list the right ascensions as well as the declinations of the stars in our catalogues. The right ascension of the First Point of Aries is, of course, \(0^h\).
I have hinted in the last paragraph that the right ascension of a star, although it doesn’t change “very much” during a night, does change quite perceptibly over a year. We shall have to return to this point later. I have not as yet precisely defined where the point \(\Upsilon\) is or how it is defined, but we shall later learn that it is not quite fixed on the equator, but it moves slightly in a manner that I shall have to describe in due course. Thus the entire system of equatorial coordinates, and the right ascensions and declinations of the stars, depends on where this mysterious First Point of Aries is. For that reason, it is always necessary to state the epoch to which right ascensions and declinations are referred. For much of the twentieth century, equatorial coordinates were referred to the epoch \(1950.0\) (strictly it was \(\text{B}1950.0\), but I shall have to postpone explaining the meaning of the prefix \(\text{B}\)). At present catalogues and atlases refer right ascensions and declinations to the epoch \(\text{J}2000.0\), where again I shall have to defer an explanation of the prefix \(\text{J}\). While there is evidently some further explanation yet to come, suffice it to say at this point that, when giving the right ascension and declination of any object, it is essential that the epoch also be given. The First Point of Aries moves very, very slowly westward relative to the stars, so that the right ascensions of all the stars are increasing at a rate of about \(0^s .008\) per day. This does not amount to much for day-to-day purposes, but it does emphasize why it is always necessary to state the epoch to which right ascensions and declinations of stars are quoted. It also means that, if you were able to observe two consecutive upper transits of \(\Upsilon\) across the meridian, the interval would be \(0^s .008\) shorter than the sidereal rotation period of Earth. It would be, in fact, \(23^\text{h} \ 56^\text{m} \ 04^\text{s} .091\). This interval between two consecutive upper meridian transits of the First Point of Aries, is called a sidereal day. (It might be thought that, since the word “sidereal” implies “relative to the stars”, this is not a particularly good term. I would have sympathy with this view, and would prefer to call the interval an “equinoctial day”. However, the term sidereal day is so firmly entrenched that I shall use that term in these notes.) A sidereal day is divided into 24 sidereal hours, which are shorter than mean solar hours by a factor of 0.99726957. We shall discuss the motion of \(\Upsilon\) in more detail in a later section. At this stage no great harm is done by considering \(\Upsilon\) in the first approximation to be fixed relative to the stars.
Now some more words. Small circles parallel to the celestial equator (such as the small circle \(\text{T}^\prime \text{XT}\) in figure \(\text{VI.2}\)) are parallels of declination. Great circles that pass through the north and south celestial poles (for example the great circle \(\text{PXBQ}\) of figure \(\text{VI.2}\)) and which are fixed on and rotate with the celestial sphere are called by a variety of names. Some call them declination circles, because you measure declination up and down these circles. Others call them hour circles, because the hour angle or right ascension is constant along them. For those who find it confusing that a given circle can be called either a declination circle or an hour circle, you can get around this difficulty by calling them colures. The colure that passes through the First Point of Aries and the diametrically opposite point on the celestial sphere, and which therefore has right ascensions \(0^h\) and \(12^h\), is the equinoctial colure. The colure that is \(90^\circ\) from this (or, rather, 6 hours from this) and which has right ascensions \(6^\text{h}\) and \(18^\text{h}\), is the solstitial colure.
The time that has elapsed, in sidereal hours, since the First Point of Aries transited (upper transit) the meridian, that is to say the hour angle of the first point of Aries, or the angle from \(\text{A}\) to \(\Upsilon\) in figure \(\text{VI.2}\), is called the Local Sidereal Time. It is evident from figure \(\text{VI.2}\) that the Local Sidereal Time is also equal to \(\Upsilon \text{B} + \text{AB}\). But \(\Upsilon \text{B}\) is the right ascension of the star \(\text{X}\) and \(\text{AB}\) is its hour angle. Therefore the local sidereal time (the hour angle of the First Point of Aries) is equal to the right ascension of any star plus its hour angle.
The sidereal time at the longitude of Greenwich (\(0^\circ\) longitude) is tabulated daily in the Astronomical Almanac and the local sidereal time at your location is equal to the local sidereal time at Greenwich minus your geographical longitude. Most observatories have two clocks running in the dome at all times. One gives Universal Time, while the other, which runs a little faster, gives the local sidereal time. But you always have a sidereal clock available, for a glance at figure \(\text{VI.2}\) will tell you that the local sidereal time is equal to the right ascension of stars at upper meridian transit.


