3.5: Spherical Triangles
- Page ID
- 6802
As with plane triangles, we denote the three angles by \(A, \ B, \ C\) and the sides opposite to them by \(a, \ b, \ c\). We are fortunate in that we have four formulas at our disposal for the solution of a spherical triangle, and, as with plane triangles, the art of solving a spherical triangle entails understanding which formula is appropriate under given circumstances. Each formula contains four elements (sides and angles), three of which, in a given problem, are assumed to be known, and the fourth is to be determined.
Three important points are to be noted before we write down the formulas.
- The formulas are valid only for triangles in which the three sides are arcs of great circles. They will not do, for example, for a triangle in which one side is a parallel of latitude.
- The sides of a spherical triangle, as well as the angles, are all expressed in angular measure (degrees and minutes) and not in linear measure (metres or kilometres). A side of \(50^\circ\) means that the side is an arc of a great circle subtending an angle of \(50^\circ\) at the centre of the sphere.
- The sum of the three angles of a spherical triangle add up to more than \(180^\circ\).
In this section are now given the four formulas without proof, the derivations being given in a later section. The four formulas may be referred to as the sine formula, the cosine formula, the polar cosine formula, and the cotangent formula. Beneath each formula is shown a spherical triangle in which the four elements contained in the formula are highlighted.
The sine formula: \[\frac{\sin a}{\sin A} = \frac{\sin b}{\sin B} \left( = \frac{\sin c}{\sin C} \right) \label{3.5.1} \tag{3.5.1}\]
\(\text{FIGURE III.10}\)
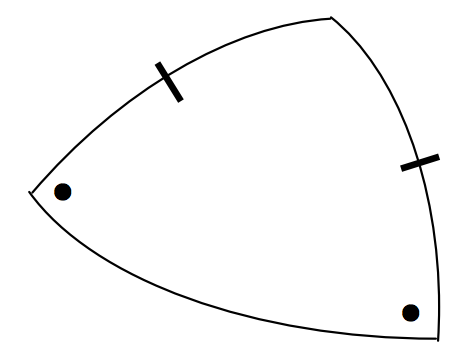
The cosine formula: \[\cos a = \cos b \cos c + \sin b \sin c \cos A \label{3.5.2} \tag{3.5.2}\]
\(\text{FIGURE III.11}\)
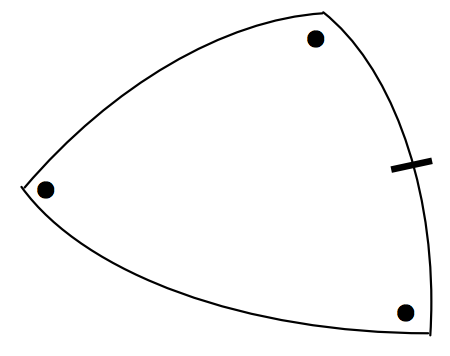
The polar cosine formula: \[\cos A = - \cos B \cos C + \sin B \sin C \cos a \label{3.5.3} \tag{3.5.3}\]
\(\text{FIGURE III.12}\)
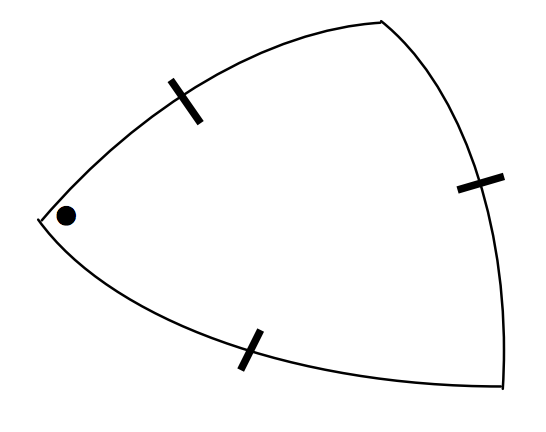
The cotangent formula: \[\cos b \cos A = \sin b \cot c - \sin A \cot C \label{3.5.4} \tag{3.5.4}\]
\(\text{FIGURE III.13}\)
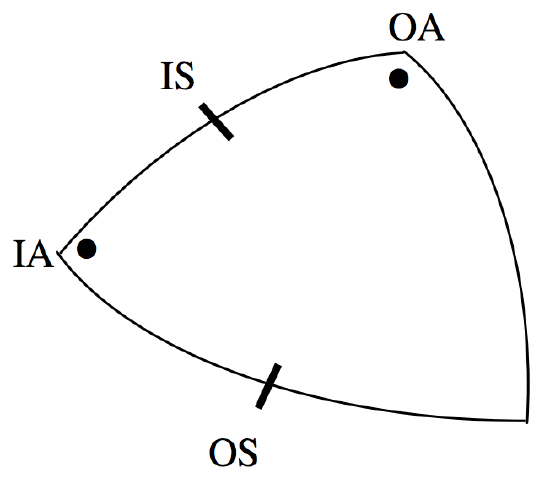
The cotangent formula is a particularly useful and frequently needed formula, and it is unfortunate that it is not only difficult to commit to memory but, even with the formula written out in front of one, it is often difficult to decide which is \(b\), which is \(A\) and so on. However, it should be noted from the drawing that the four elements, side-angle-side-angle, lie adjacent to each other in the triangle, and they may be referred to as outer side (\(\text{OS}\)), inner angle (\(\text{IA}\)), inner side (\(\text{IS}\)) and outer angle (\(\text{OA}\)) respectively. Many people find that the formula is much easier to use when written in the form
\[\cos (\text{IS}) \cos (\text{IA}) = \sin (\text{IS}) \cot (\text{OS}) - \sin (\text{IA}) \cot (\text{OA}) \label{3.5.5} \tag{3.5.5}\]
The reader will shortly be offered a goodly number of examples in the use of these formulas. However, during the course of using the formulas, it will be found that there is frequent need to solve deceptively simple trigonometric Equations of the type
\[4.737 \sin θ + 3.286 \cos θ = 5.296 \label{3.5.6} \tag{3.5.6}\]
After perhaps a brief pause, one of several methods may present themselves to the reader - but not all methods are equally satisfactory. I am going to suggest four possible ways of solving this Equation. The first method is one that may occur very quickly to the reader as being perhaps rather obvious - but there is a cautionary tale attached to it. While the method may seem very obvious, a difficulty does arise, and the reader would be advised to prefer one of the less obvious methods. There are, incidentally, two solutions to the Equation between \(0^\circ\) and \(360^\circ\). They are \(31^\circ 58^\prime .6\) and \(78^\circ 31^\prime .5\).
Method i
The obvious method is to isolate \(\cos θ\) :
\[\cos θ = 1.611 \ 686 - 1.441 \ 570 \ \sin θ.\]
Although the constants in the problem were given to four significant figures, do not be tempted to round off intermediate calculations to four. It is a common fault to round off intermediate calculations prematurely. The rounding-off can be done at the end.
Square both sides, and write the left hand side, \(\cos^2 θ\), as \(1 − \sin^2 θ\). We now have a quadratic Equation in \(\sin θ\) :
\[3.078 \ 125 \sin^2 θ - 4.646 \ 717 \sin θ + 1.597 \ 532 = 0. \]
The two solutions for \(\sin θ\) are \(0.529 \ 579\) and \(0.908 \ 014\) and the four values of \(θ\) that satisfy these values of \(\sin θ\) are \(31^\circ 58^\prime .6, \ 148^\circ \ 01^\prime .4, \ 78^\circ \ 31^\prime .5\) and \(101^\circ 28^\prime .5\).
Only two of these angles are solutions of the original Equation. The fatal move was to square both sides of the original Equation, so that we have found solutions not only to
\[\cos θ = 1.611 \ 686 - 1.441 \ 570 \sin θ\]
but also to the different Equation
\[-\cos θ = 1.611 \ 686 - 1.441 \ 570 \ \sin θ.\]
This generation of extra solutions always occurs whenever we square an Equation. For this reason, method (i), however tempting, should be avoided, particularly when programming a computer to carry out a computation automatically and uncritically.
If in doubt whether you have obtained a correct solution, substitute your solution in the original Equation. You should always do this with any Equation of any sort, anyway.
Method ii
This method makes use of the identities
\[\sin θ = \frac{2t}{1+t^2}, \quad \cos θ = \frac{1-t^2}{1+t^2},\]
where \(t = \tan \frac{1}{2} θ\).
When applied to the original Equation, this results in the quadratic Equation in \(t\):
\[8.582t^2 - 9.474t + 2.010 = 0\]
with solutions \[t= 0.286528 \quad \text{and} \quad t = 0.817410\]
The only values of \(θ\) between \(0^\circ\) and \(360^\circ\) that satisfy these are the two correct solutions \(31^\circ \ 58^\prime .6\) and \(78^\circ \ 31^\prime .5\).
It is left as an exercise to show, using this method algebraically, that the solutions to the Equation
\[a \sin θ + b \cos θ = c\]
are given by \[\tan \frac{1}{2} θ = \frac{a \pm \sqrt{a^2 + b^2 - c^2}}{b+ c}.\]
This shows that there are no real solutions if \(a^2 + b^2 < c^2\), one real solution if \(a^2 + b^2 = c^2\), and two real solutions if \(a^2 + b^2 > c^2\).
Method iii
We divide the original Equation
\[4.737 \sin θ + 3.286 \cos θ = 5.296\]
by the "hypotenuse" of \(4.737\) and \(3.286\); that is, by \(\sqrt{(4.737^2 + 3.286^2)} = 5.765151\).
Thus \[0.821 \ 661 \ \sin θ + 0.569 \ 976 \cos θ = 0.918 \ 623 \]
Now let \(0.821 \ 661 = \cos α\) and \(0.569 976 = \sin α\) (which we can, since these numbers now satisfy \(\sin^2 α \cos^2 α = 1\)) so that \(α = 34^\circ \ 44^\prime .91\).
We have \[\cos α \sin θ + \sin α \cos θ = 0.918 \ 623 \]
or \[\sin(θ + α) = 0.918623\]
from which \[θ + α = 66^\circ \ 43^\prime .54 \text{ or } 113^\circ \ 16^\prime .46\]
Therefore \[θ = 31^\circ \ 58^\prime .6 \text{ or } 78^\circ \ 31^\prime .5\]
Method iv
Methods ii and iii give explicit solutions, so there is perhaps no need to use numerical methods. Nevertheless, the reader might like to solve, by Newton-Raphson iteration, the Equation
\[f(θ) = a \sin θ + b \cos θ - c = 0,\]
for which \[f^\prime ( θ ) = a \cos θ - b \sin θ.\]
Using the values of \(a, \ b\) and \(c\) from the example above and using the Newton-Raphson algorithm, we find with a first guess of \(45^\circ\) the following iterations, working in radians:
\begin{array}{c c c}
0.785 \ 398 \\
0.417 \ 841 \\
0.541 \ 499 \\
0.557 \ 797 \\
0.558 \ 104 \\
0.558 \ 104 & = & 31^\circ 58^\prime .6 \\
\end{array}
The reader should verify this calculation, and, using a different first guess, show that NewtonRaphson iteration quickly leads to \(78^\circ \ 31^\prime .5\).
Having now cleared that small hurdle, the reader is invited to solve the spherical triangle problems below. Although these twelve problems look like pointless repetitive work, they are in fact all different. Some have two solutions between \(0^\circ\) and \(360^\circ\) ; others have just one. After solving each problem, the reader should sketch each triangle - especially those that have two solutions - in order to see how the two-fold ambiguities arise. The reader should also write a computer program that will solve all twelve types of problem at the bidding of the user. Answers should be given in degrees, minutes and tenths of a minute, and should be correct to that precision. For example, the answer to one of the problems is \(47^\circ \ 37^\prime .3\). An answer of \(47^\circ \ 37^\prime .2\) or \(47^\circ \ 37^\prime .4\) should be regarded as wrong. In celestial mechanics, there is no place for answers that are "nearly right". An answer is either right or it is wrong. (This does not mean, of course, that an angle can be measured with no error at all; but the answer to a calculation given to a tenth of an arcminute should be correct to a tenth of an arcminute.)
All angles and sides in degrees
\begin{array}{c c c c c}
10. & a=64 & b=33 & c=37 & C = ? \\
11. & a=39 & b=48 & C=74 & c = ? \\
12. & a=16 & b=37 & C=42 & B= ? \\
13. & a=21 & b=43 & A=29 & c=? \\
14. & a=67 & b=54 & A=39 & B=? \\
15. & a=49 & b=59 & A=14 & C=? \\
16. & A=24 & B=72 & c=19 & a=? \\
17. & A=79 & B=84 & c=12 & C=? \\
18. & A=62 & B=49 & a=44 & b=? \\
19. & A=59 & B=32 & a=62 & c=? \\
20. & A=47 & B=57 & a=22 & C=? \\
21. & A=79 & B=62 & C=48 & c=? \\
\end{array}
Solutions
10. \(28^\circ 18^\prime .2\)
11. \(49^\circ 32^\prime .4\)
12. \(117^\circ 31^\prime .0\)
13. \(30^\circ 46^\prime .7 \text{ or } 47^\circ 37^\prime .3\)
14. \(33^\circ 34^\prime .8\)
15. \(3^\circ 18^\prime .1 \text{ or } 162^\circ 03^\prime .9\)
16. \(7^\circ 38^\prime .2\)
17. \(20^\circ 46^\prime .6\)
18. \(36^\circ 25^\prime .5\)
19. \(76^\circ 27^\prime .7\)
20. \(80^\circ 55^\prime .7 \text{ or } 169^\circ 05^\prime .2\)
21. \(28^\circ 54^\prime .6\)
Derivation of the formulas
Before moving on to further problems and applications of the formulas, it is time to derive the four formulas which, until now, have just been given without proof. We start with the cosine formula. There is no loss of generality in choosing rectangular axes such that the point \(\text{A}\) of the spherical triangle \(\text{ABC}\) is on the \(z\)-axis and the point \(\text{B}\) and hence the side \(c\) are in the \(zx\)-plane. The sphere is assumed to be of unit radius.
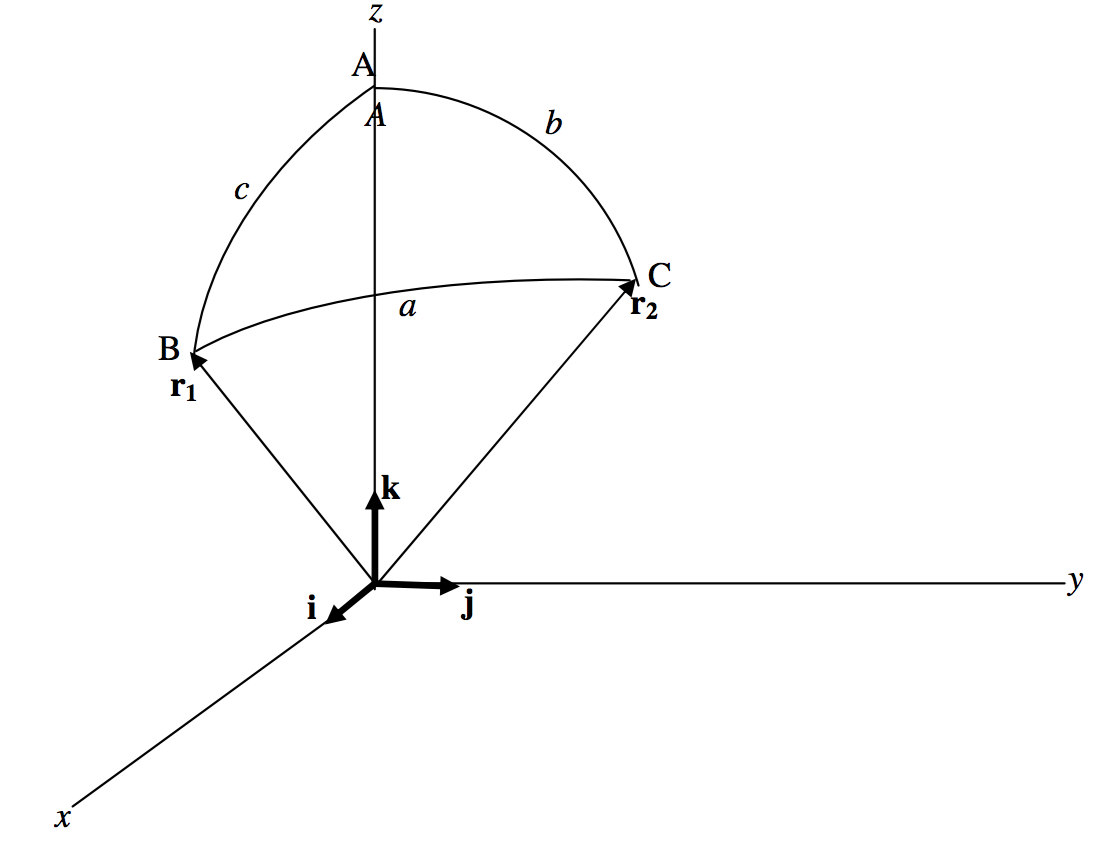
\(\text{FIGURE III.14}\)
If \(\textbf{i}, \ \textbf{j}\) and \(\textbf{k}\) are unit vectors directed along the \(x\)−, \(y\)− and \(z\)−axes respectively, inspection of the figure will show that the position vectors of the points \(\text{B}\) and \(\text{C}\) with respect to the centre of the sphere are
\[\textbf{r}_1 = \textbf{i} \sin c + \textbf{k} \cos c \label{3.5.7} \tag{3.5.7}\]
and \[\textbf{r}_2 = \textbf{i} \sin b \cos A + \textbf{j} \sin b \sin A + \textbf{k} \cos b \label{3.5.8} \tag{3.5.8}\]
respectively.
The scalar product of these vectors (each of magnitude unity) is just the cosine of the angle between them, namely \(\cos a\), from which we obtain immediately
\[\cos a = \cos b \cos c + \sin b \sin c \cos A. \label{3.5.9} \tag{3.5.9}\]
To obtain the sine formula, we isolate \(\cos A\) from this Equation, square both sides, and write \(1 − \sin^2 A\) for \(\cos^2 A\). Thus,
\[(\sin b \sin c \cos A )^2 = (\cos a - \cos b \cos c )^2 , \label{3.5.10} \tag{3.5.10}\]
and when we have carried out these operations we obtain
\[\sin^2 A = \frac{\sin^2 b \sin^2 c - \cos^2 a - \cos^2 b \cos^2 c + 2\cos a \cos b \cos c}{\sin^2 b \sin^2 c} . \label{3.5.11} \tag{3.5.11}\]
In the numerator, write \(1 − \cos^2 b\) for \(\sin^2 b\) and \(1 − \cos^2 c\) for \(\sin^2 c\), and divide both sides by \(\sin^2 a\). This results in
\[\frac{\sin^2 A}{\sin^2 a} = \frac{1-\cos^2 a - \cos^2 b - \cos^2 c + 2\cos a \cos b \cos c}{\sin^2 a \sin^2 b \sin^2 c}. \label{3.5.12} \tag{3.5.12}\]
At this stage the reader may feel that we are becoming bogged down in heavier and heavier algebra and getting nowhere. But, after a careful look at Equation \(\ref{3.5.12}\), it may be noted with some delight that the next line is:
Therefore \[\frac{\sin A}{\sin a} = \frac{\sin B}{\sin b} = \frac{\sin C}{\sin c}. \label{3.5.13} \tag{3.5.13}\]
The derivation of the polar cosine formula may also bring a small moment of delight. In figure \(\text{III.15}\), \(\text{A}^\prime \text{B}^\prime \text{C}^\prime\) is a spherical triangle. \(\text{ABC}\) is also a spherical triangle, called the polar triangle to \(\text{A}^\prime \text{B}^\prime \text{C}^\prime\). It is formed in the following way. The side \(\text{BC}\) is an arc of a great circle \(90^\circ\) from \(\text{A}^\prime\); that is, \(\text{BC}\) is part of the equator of which \(\text{A}^\prime\) is pole. Likewise \(\text{CA}\) is \(90^\circ\) from \(\text{B}^\prime\) and \(\text{AB}\) is \(90^\circ\) from \(\text{C}^\prime\). In the drawing, the side \(\text{B}^\prime \text{C}^\prime\) of the small triangle has been extended to meet the sides \(\text{AB}\) and \(\text{CA}\) of the large triangle. It will be evident from the drawing that the angle \(A\) of the large
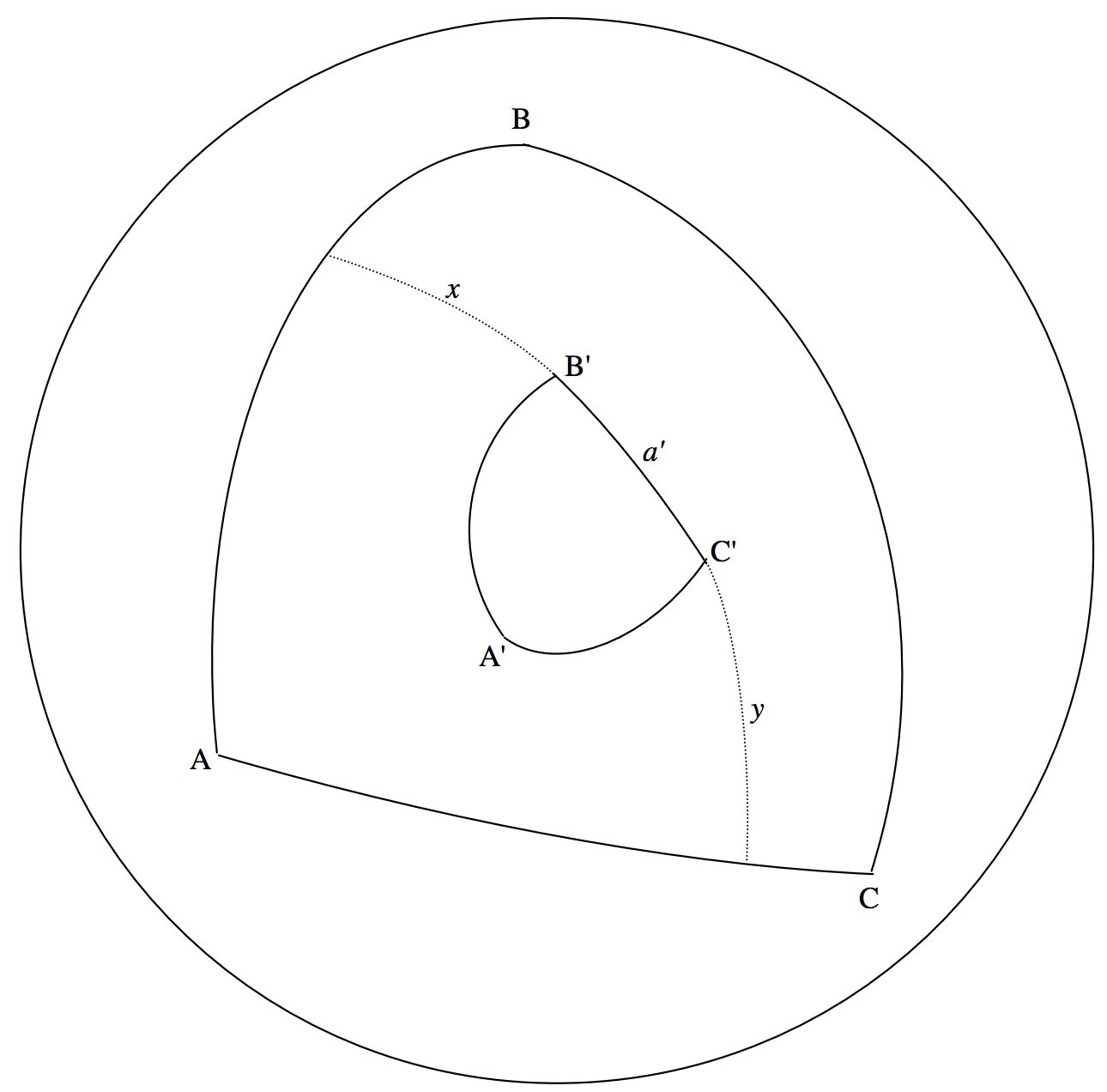
\(\text{FIGURE III.15}\)
triangle is equal to \(x + a^\prime + y\). Further, from the way in which the triangle \(\text{ABC}\) was formed, \(x+ a^\prime\) and \(a^\prime + y\) are each equal to \(90^\circ\). From these relations, we see that
\[A + A = [(x + a^\prime) + y] + [x + (a^\prime + y)]\]
or \[2A = 180^\circ + x + y = 180^\circ + A - a^\prime \]
Therefore \[A = 180^\circ - a^\prime\]
In a similar manner, \[B = 180^\circ - b^\prime \text{ and } C = 180^\circ - c^\prime\]
Now, suppose \(f(A^\prime, B^\prime, C^\prime, a^\prime, b^\prime, c^\prime) = 0\) is any relation between the sides and angles of the triangle \(\text{A}^\prime \text{B}^\prime \text{C}^\prime\). We may replace \(a^\prime\) by \(180^\circ − A, \ b^\prime\) by \(180^\circ − B\), and so on, and this will result in a relation between \(A, \ B, \ C, \ a, \ b\) and \(c\) ; that is, it will result in a relation between the sides and angles of the triangle \(\text{ABC}\).
For example, the Equation
\[\cos a^\prime = \cos b^\prime \cos c^\prime + \sin b^\prime \sin c^\prime \cos A^\prime \label{3.5.14} \tag{3.5.14}\]
is valid for the triangle \(\text{A}^\prime \text{B}^\prime \text{C}^\prime\). By making these substitutions, we find the following formula valid for triangle \(\text{ABC}\):
\[- \cos A = \cos B \cos C - \sin B \sin C \cos a, \label{3.5.15} \tag{3.5.15}\]
which is the polar cosine formula.
The reader will doubtless like to try starting from the sine and cotangent formulas for the triangle \(\text{A}^\prime \text{B}^\prime \text{C}^\prime\) and deduce corresponding polar formulas for the triangle \(\text{ABC}\), though this, unfortunately, may give rise to some anticlimactic disappointment.
I know of no particularly interesting derivation of the cotangent formula, and I leave it to the reader to work through the rather pedestrian algebra. Start from
\[\cos a = \cos b \cos c + \sin b \sin c \cos A\]
and \[\cos c = \cos a \cos b + \sin a \sin b \cos C.\]
Eliminate \(\cos c\) (but retain \(\sin c\)) from these Equations, and write \(1 − \sin^2 b\) for \(\cos^2 b\). Finally substitute \(\frac{\sin c \sin A}{\sin C}\) for \(\sin a\), and, after some tidying up, the cotangent formula should result.
At this stage, we have had some practice in solving the four spherical triangle formulas, and we have derived them. In this section we encounter examples in which the problem is not merely to solve a triangle, but to gain some experience in setting up a problem and deciding which triangle has to be solved.
The coordinates of the Dominion Astrophysical Observatory, near Victoria, British Columbia, are
Latitude \(48^\circ 31^\prime .3 \text{N}\) Longitude \(123^\circ 25^\prime .0 \text{W}\)
and the coordinates of the David Dunlap Observatory, near Toronto, Ontario, are
Latitude \(43^\circ 51^\prime .8 \text{N}\) Longitude \( 79^\circ 25^\prime .3 \text{W}\)
How far is Toronto from Victoria, and what is the azimuth of Toronto relative to Victoria?
The triangle to be drawn and solved is the triangle \(\text{PVT}\), where \(\text{P}\) is the Earth's north pole, \(\text{V}\) is Victoria, and \(\text{T}\) is Toronto. On figure \(\text{III.16}\) are marked the colatitudes of the two cities and the difference between their longitudes.
The great circle distance \(ω\) between the two observatories is easily given by the cosine formula:
\[\cos ω = \cos 41^\circ 28^\prime .7 \cos 46^\circ 08^\prime .2 + \sin 41^\circ 28^\prime .7 \sin 46^\circ 08^\prime .2 \cos 43^\circ 59^\prime .7\]
From this, we find \(ω = 30^\circ 22^\prime .7\) or \(0.53021\) radians. The radius of the Earth is \(6371 \ \text{km}\), so the distance between the observatories is \(3378 \ \text{km}\) or \(2099\) miles.
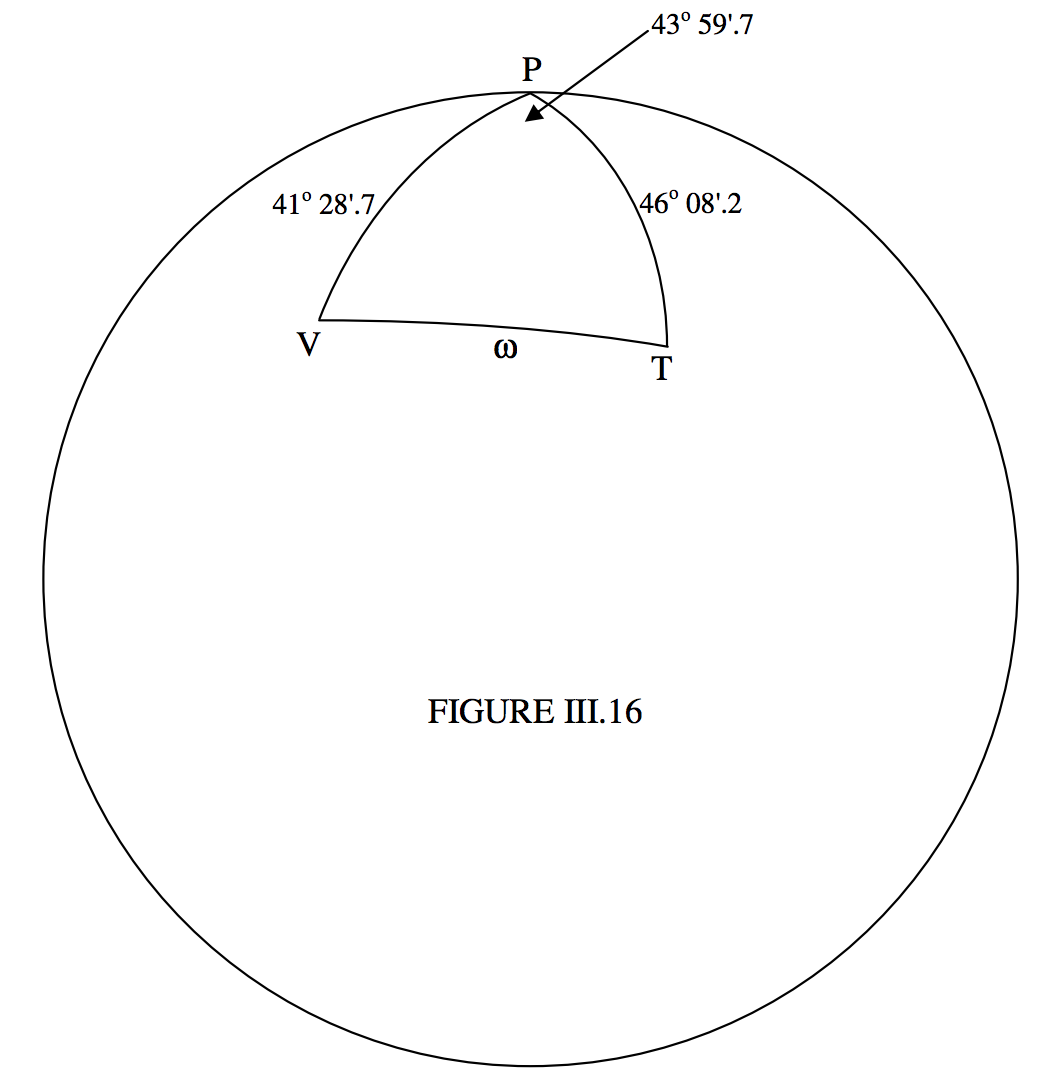
Now that we have found \(ω\), we can find the azimuth, which is the angle \(V\), from the sine formula:
\[\sin V = \frac{\sin 46^\circ 08^\prime .2 \ \sin 43^\circ 59^\prime .7}{\sin 30^\circ 22^\prime .7} = 0.990 \ 275\]
and hence \[V = 82^\circ 00^\prime .3\]
But we should now remember that \(\sin^{-1} 0.990 \ 275\) has two values between \(0^\circ\) and \(180^\circ\), namely \(82^\circ 00^\prime .3\) and \(97^\circ 59^\prime .7\).
Usually it is obvious from inspection of a drawing which of the two values of \(\sin^{-1}\) is the required one. Unfortunately, in this case, both values are close to \(90^\circ\), and it may not be immediately obvious which of the two values we require. However, it will be noticed that Toronto has a more southerly latitude than Victoria, and this should easily resolve the ambiguity.
We could, of course, have found the azimuth \(V\) by using the cotangent formula, without having to calculate \(ω\) first. Thus
\[\cos 41^\circ 28^\prime .7 \cos 43^\circ 59^\prime .7 = \sin 41^\circ 28^\prime .7 \cot 46^\circ 08^\prime .2 - \sin 43^\circ 59^\prime .7 \cot V\]
There is only one solution for \(V\) between \(0^\circ\) and \(180^\circ\), and it is the correct one, namely \(82^\circ 00^\prime .3\). A good drawing will show the reader why the correct solution was the acute rather than the obtuse angle (in our drawing the angle was made to be close to \(90^\circ\) in order not to bias the reader one way or the other), but in any case all readers, especially those who were trapped into choosing the obtuse angle, should take careful note of the difficulties that can be caused by the ambiguity of the function \(\sin^{-1}\). Indeed it is the strong advice of the author never to use the sine formula, in spite of the ease of memorizing it. The cotangent formula is more difficult to commit to memory, but it is far more useful and not so prone to quadrant mistakes.
Consider two points, \(\text{A}\) and \(\text{B}\), at latitude \(20^\circ \text{N}\), longitude \(25^\circ \text{E}\), and latitude \(72^\circ \text{N}\), longitude \(44^\circ \text{E}\). Where are the poles of the great circle passing through these two points? We shall present two methods of doing the problem. First, by solving spherical triangles. And second, kindly suggested to me by Achintya Pal, using the methods of algebraic coordinate geometry.
Let us call the colatitude and longitude of the first point \((θ_1 , \phi_1)\) and of the second point \((θ_2, \phi_2)\) We shall consider the question answered if we can find the coordinates \((θ_0, \phi_0)\) of the poles \(\text{Q}\) and \(\text{Q}^\prime\) of the great circle passing through the two points. In figure \(\text{III.17}\), \(\text{P}\) is the north pole of the Earth, \(\text{A}\) and \(\text{B}\) are the two points in question, and \(\text{Q}\) is one of the two poles of the great circle joining \(\text{A}\) and \(\text{B}\). The figure also shows the triangle \(\text{PQA}\). We’ll suppose that the origin for longitudes (“Greenwich”) is behind the plane of the paper. The east longitudes of \(\text{Q}\), \(\text{A}\) and \(\text{B}\) are, respectively, \(\phi_0, \phi_1, \phi_2\); and their colatitudes are \(θ_0 , θ_1 ,θ_2\).
\[0=\cos θ_0 \cos θ_1 + \sin θ_0 \sin θ_1 \cos (\phi_1 - \phi_0), \label{3.5.16} \tag{3.5.16}\]
from which
\[\tan θ_0 = -\frac{1}{\tan θ_1 \cos (\phi_1 - \phi_0)}. \label{3.5.17} \tag{3.5.17}\]
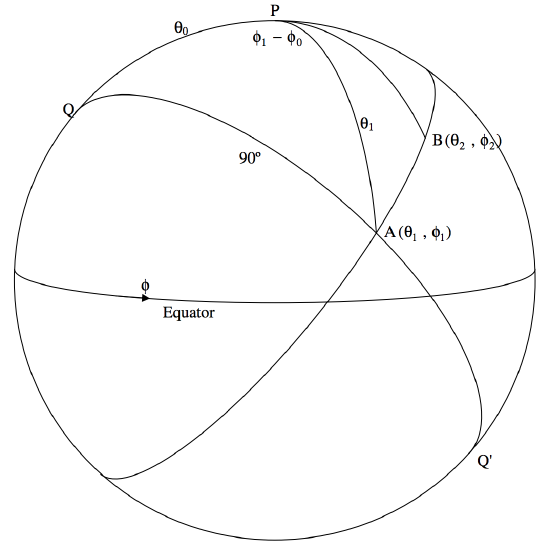
\(\text{FIGURE III.17}\)
Similarly from triangle \(\text{PQB}\) we would obtain
\[\tan θ_0 = -\frac{1}{\tan θ_2 \cos(\phi_2 - \phi_0)}. \label{3.5.18} \tag{3.5.18}\]
These are two Equations in \(θ_0\) and \(\phi_0\), so the problem is in principle solved. Equate the righthand sides of the two Equations, expand the terms \(\cos (\phi_1 - \phi_0 )\) and \(\cos (\phi_2 - \phi_0 )\), gather the terms in \(\sin \phi_0\) and \(\cos \phi_0\), eventually to obtain
\[\tan \phi_0 = \frac{\tan θ_1 \cos \phi_1 - \tan θ_2 \cos \phi_2}{\tan θ_2 \sin \phi_2 - \tan θ_1 \sin \phi_1}. \label{3.5.19} \tag{3.5.19}\]
If we substitute the angles given in the original problem, we obtain
\[\tan \phi_0 = \frac{\tan 70^\circ \cos 25^\circ - \tan 18^\circ \cos 44^\circ}{\tan 18^\circ \sin 44^\circ - \tan 70^\circ \sin 25^\circ} = -2.412 \ 091 \ 0\]
from which \[\phi_0 = 112^\circ 31^\prime .1 \quad \text{or} \quad 292^\circ 31^\prime .1\]
Note that we get two values for \(\phi_0\) differing by \(180^\circ\), as expected.
We then use either of the Equations for \(\tan θ_0\) to obtain \(θ_0\) (It is good practice to use both of them as a check on the arithmetic.) The north polar distance, or colatitude, must be between \(0^\circ\) and \(180^\circ\), so there is no ambiguity of quadrant.
With \(\phi_0 = 112^\circ 31^\prime .1\), we obtain \(θ_0 = 96^\circ 47^\prime .1\), i.e. latitude \(6^\circ 47^\prime .1 \ \text{S}\).
and with \(\phi_0 = 292^\circ 31^\prime .1\), we obtain \(θ_0 = 83^\circ 12^\prime .9\), i.e. latitude \(6^\circ 47^\prime .1 \ \text{N}\).
and these are the coordinates of the two poles of the great circle passing through \(\text{A}\) and \(\text{B}\). The reader is strongly urged actually to carry out these computations numerically in order to be quite sure that the quadrants are correct and unambiguous. Indeed, dealing with the quadrant problem may be regarded as the most important part of the exercise.
We arrived at Equation \(\ref{3.5.17}\) and \(\ref{3.5.18}\) by solving two spherical triangles by the methods of spherical trigonometry. The second method, suggested, as mentioned above, by Achintya Pal, uses the methods of algebraic coordinate geometry in three dimensions to arrive at the same Equations. We refer coordinates to axes \(\text{O}xyz\). \(\text{O}\) is the centre of the Earth, taken to be of unit radius. \(\text{OP}\) is the \(z\)-axis. The \(\text{O}x\) and \(\text{O}y\) axes are not drawn in figure \(\text{III.17}\), but the \(x\)-axis may be taken to be directed somewhere to the rear of the drawing (away from the reader), and the \(y\)-axis somewhere in the front of the drawing, both being, of course, in the plane of the equator.
Let us write the Equation to the plane containing \(\text{A}\) and \(\text{B}\) in the form
\[lx + my + nz = 0 \label{3.5.20} \tag{3.5.20}\]
Here \((l,m,n)\) are the direction cosines of the normal to the plane \(\text{AB}\), and are given by
\[l = \sin θ_0 \cos \phi_0 \quad m = \sin θ_0 \sin \phi_0 \quad n = \cos θ_0 \label{3.5.21a,b,c} \tag{3.5.21a,b,c}\]
The \((x,y,z)\) coordinates of the point \(\text{A}\) are
\[x = \sin θ_1 \cos \phi_1 \quad y = \sin θ_1 \sin \phi_1 \quad x= \cos θ_1 \label{3.5.22a,b,c} \tag{3.5.22a,b,c}\]
On substitution of Equations \(\ref{3.5.21a,b,c}\) and \(\ref{3.5.22a,b,c}\) into Equation \(\ref{3.5.20}\) we obtain:
\[\sin θ_0 \cos \phi_0 \sin θ_1 \cos \phi_1 + \sin θ_0 \sin \phi_0 \sin θ_1 \sin \phi_1 + \cos θ_0 \cos θ_1 = 0 \label{3.5.23} \tag{3.5.23}\]
After some very modest algebraic manipulation (e.g., start by dividing by \(\sin θ_1 \cos θ_0\)) we very soon arrive again at Equation \(\ref{3.5.17}\), and in a similar manner at Equation \(\ref{3.5.18}\).
As a bonus we note that any point having spherical coordinates \((θ, \phi)\) lying on the great circle whole pole is at \(( θ_0 , \phi_0)\) satisfies the Equation
\[\cot θ = - \tan θ_0 \cos (\phi - \phi) \label{3.5.24} \tag{3.5.24}\]
This Equation may be regarded as the \((θ, \phi)\) Equation to the great circle \(\text{AB}\), and it answers the problem converse to the one originally posed: What is the Equation to the great circle whose pole is at \((θ_0, \phi_0\)) ?
Here is a challenging exercise and an important one in meteor astronomy. Two shower meteors are seen, diverging from a common radiant. One starts at right ascension 6 hours, declination +65 degrees, and finishes at right ascension 1 hour, declination +75 degrees. The second starts at right ascension 5 h, declination +35 degrees, and finishes at right ascension 3 hours, declination +15 degrees. Where is the radiant?
The assiduous student will make a good drawing of the celestial sphere, illustrating the situation as accurately as possible. The calculation will require some imaginative manipulation of spherical triangles. After arriving at what you believe to be the correct answer, look at your drawing to see whether it is reasonable. The next step might be to develop a general trigonometrical expression for the answer in terms of the original data, or to program the calculation for a computer, so that it is henceforth available for any similar calculation. Or one can go yet further, and write a computer program that will give a least-squares solution for the radiant for many more than two meteors in the shower. I find for the answer to the above problem that the radiant is at right ascension 7.26 hours and declination +43.8 degrees.
Uniqueness of Solutions
The reader who has by now worked through a variety of problems in the solution of a triangle will have noticed that, given three elements of a triangle, sometimes there is a unique solution, whereas sometimes there are two possible triangles that satisfy the original data. Yet again, it may sometimes be found that there is no possible solution, meaning that there is no possible triangle that satisfies the given data, which must therefore be presumed incorrect. I am very much indebted to Alan Johnstone for lengthy discussions on this problem, and indeed for pointing out that some of the “solutions” given in an earlier version of these notes were in fact invalid (and have now been corrected). I believe the following criteria determine how many valid solutions there are for a given triplet of data, for plane triangles and for spherical triangles.
We may be given three elements of a triangle,
Thus
- Three sides: \(a, b, c,\)
- Two sides and the included angle: \(b, c, A.\)
- Two sides and a nonincluded angle: \(a, b, A.\)
- Two angles and a common side: \(a, B, C.\)
- Two angles and another side: \(A, B, a.\)
- Three angles: \(A, B, C.\)
Question:
Which of these give a unique solution, and which admit of two solutions? And which are impossible triangles? I believe the answers are as follows:
\(\textbf{Plane Triangles}\)
i. Let \(d = a + b - c, \quad e = b + c - a, \quad f = c + a - b\)
For a valid triangle, \(d, \ e\) and \(f\) must all be positive. If so, there is a unique solution.
ii. There is a unique solution.
iii. If \(a>b\) there is a unique solution.
If \(a=b\), there is a unique solution if \(A < 90^\circ\). Otherwise there is no valid triangle.
If \(a < b\) there are zero, one or two solutions, according as to whether
\(\sin A > \frac{a}{b}, \sin A = \frac{a}{b} \text{ or } \sin A < \frac{a}{b}\).
iv. There is a unique solution.
v. There is a unique solution.
vi. There is a unique solution except that only the relative lengths of the sides are determined.
\(\textbf{Spherical Triangles}\)
i. Let \(d = a + b - c, \quad e = b + c - a, \quad f = c + a - b\)
For a valid triangle, \(d, \ e\) and \(f\) must all be positive. If so, there is a unique solution.)
ii. There is a unique solution.
iii. If \(\sin A > \frac{\sin a}{\sin b}\), there is no real solution.
If \(A = a = b = 90^\circ\), then \(B = 90^\circ\), and \(c\) and \(C\) are equal but indeterminate.
Otherwise:
If \(a > b\) there is a unique solution.
If \(a = b\), there is a unique solution if \(a < 90^\circ\). Otherwise there is no real solution.
If \(a < b\) there are one or two solutions, according as to whether
\[\sin A = \frac{\sin a}{\sin b} \text{ or } \sin A < \frac{\sin a}{\sin b}.\]
iv. There is a unique solution.
v. If \(\sin A = \frac{\sin A }{\sin B}\), there is no real solution.
If \(A=B=a=90^\circ\), then \(b = 90^\circ\), and \(c\) and \(C\) are equal but indeterminate.
Otherwise:
If \(A>B\) there is a unique solution.
If \(A=B\), there is a unique solution if \(a<90^\circ\). Otherwise there is no real solution.
If \(A<B\) there are one or two solutions, according as to whether
\[\sin a = \frac{\sin A}{\sin B} \text{ or } \sin a < \frac{\sin A}{\sin B}.\]


