5.4.10: Bubble Inside a Uniform Solid Sphere
- Page ID
- 8140
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
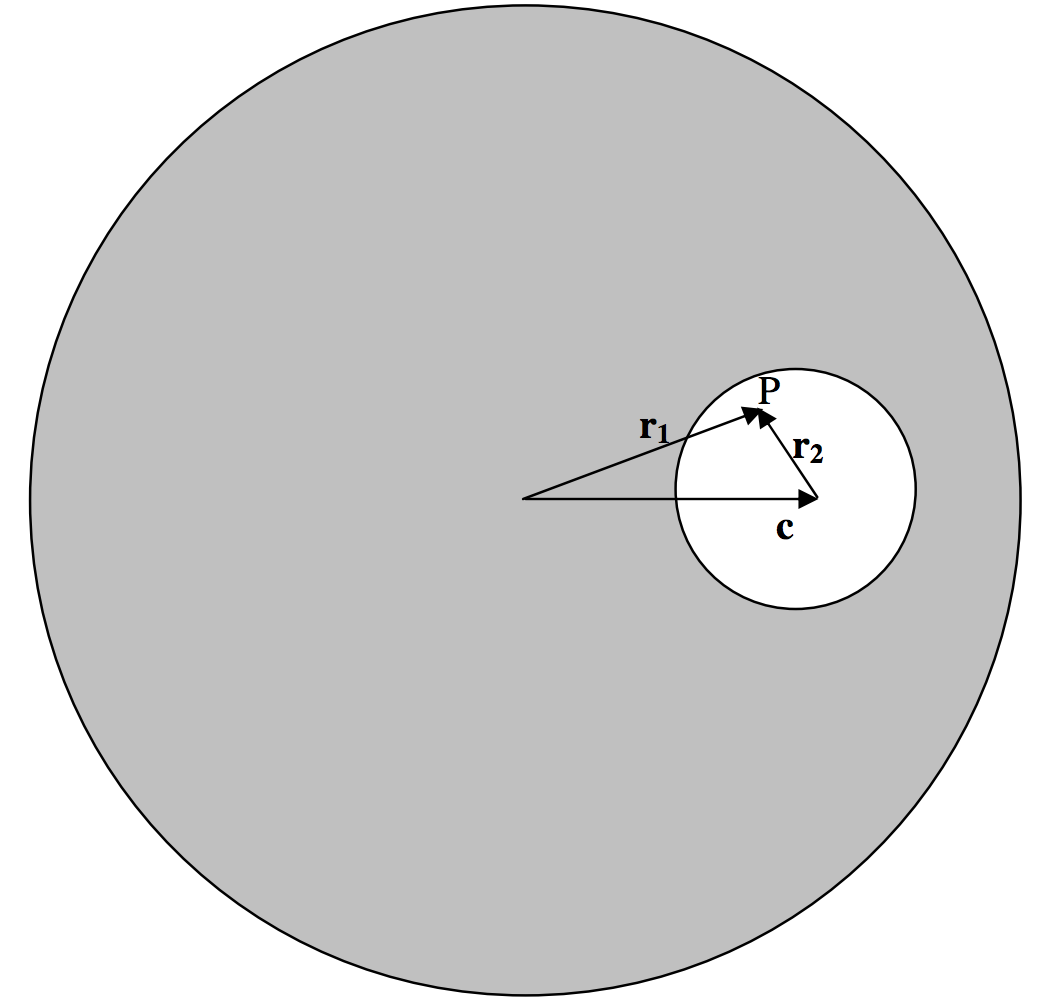
\(\text{FIGURE V.11}\)
\(\text{P}\) is a point inside the bubble. The field at \(\text{P}\) is equal to the field due to the entire sphere minus the field due to the missing mass of the bubble. That is, it is
\[\textbf{g} = -\frac{4}{3} \pi G ρ \textbf{r}_1 - (-\frac{4}{3} \pi G ρ \textbf{r}_2) = -\frac{4}{3} \pi G ρ ( \textbf{r}_1 - \textbf{r}_2) = -\frac{4}{3} \pi G ρ \textbf{c}. \label{5.4.26} \tag{5.4.26}\]
That is, the field at \(\text{P}\) is uniform (i.e. is independent of the position of \(\text{P}\)) and is parallel to the line joining the centres of the two spheres.


