5.8.6: Rods

Refer to figure $\text{V.5}$. The potential at $\text{P}$ due to the element $δx$ is $-\frac{Gλδx}{r} = − Gλ \sec θδθ$. The total potential at $\text{P}$ is therefore

$$ψ = - G λ \int_α^β \sec θdθ = - Gλ \ln \left[ \frac{\sec β + \tan β}{\sec α + \tan α} \right] . \label{5.8.15} \tag{5.8.15}$$

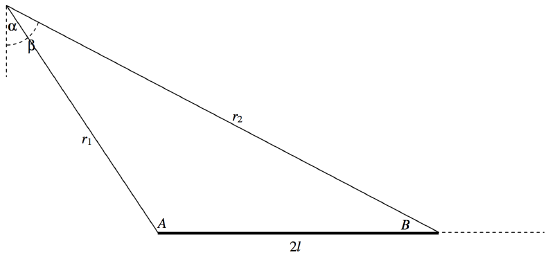
$\text{FIGURE V.24}$

Refer now to figure $\text{V.24}$, in which $A = 90^\circ + α$ and $B = 90^\circ − β$.

$$\frac{\sec β + \tan β}{\sec α + \tan α} = \frac{\cos α (1+ \sin β)}{\cos β (1 + \sin α)} = \frac{\sin A (1+ \cos B)}{\sin B(1-\cos A)} = \frac{2 \sin \frac{1}{2}A \cos \frac{1}{2} A . 2 \cos^2 \frac{1}{2} B}{2\sin \frac{1}{2} B \cos \frac{1}{2} B . 2 \sin^2 \frac{1}{2} A} = \cot \frac{1}{2} A \cot \frac{1}{2} B = \sqrt{\frac{s(s-r_2)}{(s-r_1)(s-2l)}}\cdot \sqrt{\frac{s(s-r_1)}{(s-2l)(s-r_2)}},$$

where $s = \frac{1}{2} (r_1 + r_2 + 2l)$. (You may want to refer here to the formulas on pp. 37 and 38 of Chapter 2.)

Hence $$ψ = - Gλ \ln \left[ \frac{r_1 + r_2 + 2l}{r_1 + r_2 -2l} \right]. \label{5.8.16} \tag{5.8.16}$$

If $r_1$ and $r_2$ are very large compared with $l$, they are nearly equal, so let’s put $r_1 + r_2 = 2r$ and write Equation 5.8.17 as

$$ψ = -\frac{Gm}{2l} \ln \left[ \frac{2r \left( 1 + \frac{2l}{2r} \right)}{2r \left( 1 - \frac{2l}{2r} \right)} \right] = -\frac{Gm}{2l} \left[ \ln \left(1 + \frac{l}{r} \right) - \ln \left( 1 - \frac{l}{r} \right) \right] .$$

Maclaurin expand the logarithms, and you will see that, at large distances from the rod, the potential is, expected, $−Gm/r$.

Let us return to the near vicinity of the rod and to Equation $\ref{5.8.16}$. We see that if we move around the rod in such a manner that we keep $r_1 + r_2$ constant and equal to $2a$, say − that is to say if we move around the rod in an ellipse (see our definition of an ellipse in Chapter 2, Section 2.3) − the potential is constant. In other words the equipotentials are confocal ellipses, with the foci at the ends of the rod. Equation $\ref{5.8.16}$ can be written

$$ψ = - Gλ \ln \left( \frac{a+l}{a-l} \right) . \label{5.8.17} \tag{5.8.17}$$

For a given potential $ψ$, the equipotential is an ellipse of major axis

$$2a = 2l \left( \frac{e^{ψ/(Gλ)}+1}{e^{ψ/(Gλ)}-1} \right), \label{5.8.20} \tag{5.8.20}$$

where $2l$ is the length of the rod. This knowledge is useful if you are exploring space and you encounter an alien spacecraft or an asteroid in the form of a uniform rod of length $2l$.