1.14: Relations between Flux, Intensity, Exitance, Irradiance
- Page ID
- 8000
In this section I am going to ask, and answer, three questions.
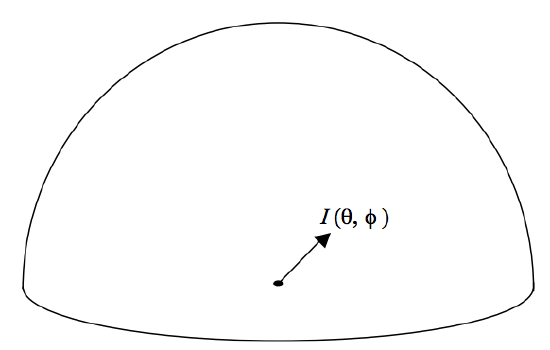
i. (See figure I.3 )
\(\text{FIGURE I.3}\)
A point source of light has an intensity that varies with direction as \(I(\theta , \phi\)). What is the radiant flux radiated into the hemisphere \(\theta < \pi /2\)? This is easy; we already answered it for a complete sphere in equation 1.6.3. For a hemisphere, the answer is
\[\phi = \int_0^{2\pi} \int_0^{\pi/2} I(\theta, \phi) \sin \theta d \theta d \phi. \tag{1.14.1} \label{1.14.1}\]
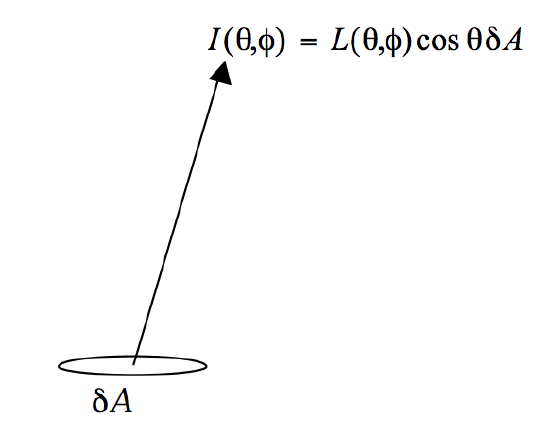
ii. At a certain point on an extended plane radiating surface, the radiance is \(L(\theta ,\phi\)). What is the emergent exitance \(M\) at that point?
\(\text{FIGURE I.4}\)
Consider an elemental area \(\delta A\) (see figure I.4). The intensity \(I( \theta , \phi\)) radiated in the direction \((\theta ,\phi )\) is the radiance times the projected area \(\cos \theta \ \delta A\). Therefore the radiant power or flux radiated by the element into the hemisphere is
\[\delta \phi = \int_0^{2\pi} \int_0^{\pi/2} L(\theta, \phi) \cos \theta \sin \theta d\theta d \phi \delta A, \tag{1.14.2} \label{1.14.2}\]
and therefore the exitance is
\[M=\int_0^{2\pi} \int_0^{\pi/2} L(\theta, \phi) \cos \theta \sin \theta d\theta d\phi \tag{1.14.3} \label{1.14.3}\]
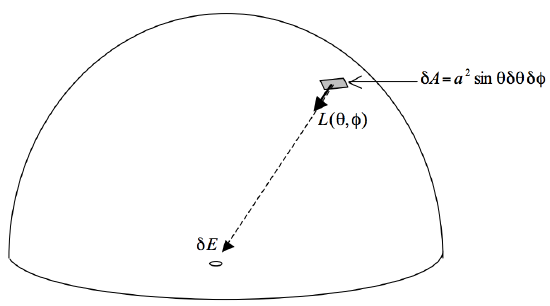
iii. A point \(O\) is at the centre of the base of a hollow radiating hemisphere whose radiance in the direction \((\theta , \phi )\) is \(L(\theta , \phi)\). What is the irradiance at that point \(O\) ? (See figure I.5.)
\(\text{FIGURE I.5}\)
Consider an elemental area \(a^2 \ \sin \theta \ \delta \theta \ \delta\phi\) on the inside of the hemisphere at a point where the radiance is \(L(\theta ,\phi )\) (figure I.5). The intensity radiated towards \(O\) is the radiance times the area:
\[\delta I (\theta, \phi) = L(\theta, \phi) a^2 \sin \theta \delta \theta \delta \phi \tag{1.14.4} \label{1.14.4}\]
The irradiance at \(O\) from this elemental area is (see equation (1.10.1)
\[\delta E = \frac{\delta I (\theta,\phi) \cos \theta}{a^2} = L (\theta, \phi) \cos \theta \sin \theta \delta \theta \delta \phi, \tag{1.14.5} \label{1.14.5}\]
and so the irradiance at O from the entire hemisphere is
\[E = \int_0^{2\pi} \int_0^{\pi/2} L(\theta, \phi) \cos \theta \sin \theta \delta \theta \delta \phi. \tag{1.14.6} \label{1.14.6}\]
The same would apply for any shape of inverted bowl - or even an infinite plane radiating surface (see figure I.6.)
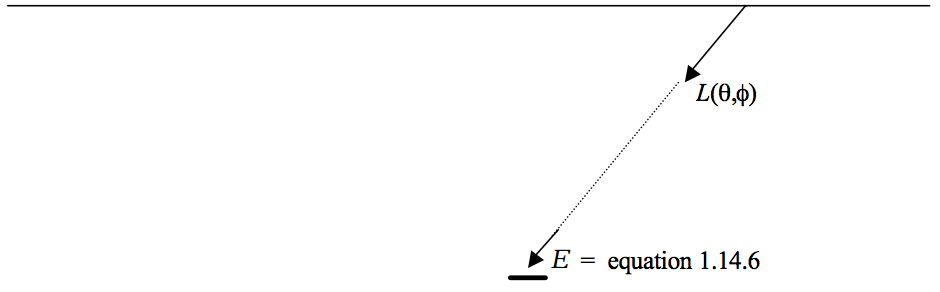
\(\text{FIGURE I.6}\)


