10.6: Translational Motion of the Center of Mass

Last updated
Save as PDF

Page ID: 24485

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The velocity of the center of mass is found by differentiation,

\[\overrightarrow{\mathbf{V}}_{\mathrm{cm}}=\frac{1}{m_{\mathrm{sys}}} \sum_{i=1}^{i=N} m_{i} \overrightarrow{\mathbf{v}}_{i}=\frac{\overrightarrow{\mathbf{p}}_{\mathrm{sys}}}{m_{\mathrm{sys}}} \nonumber \]

The momentum is then expressed in terms of the velocity of the center of mass by

\[\overrightarrow{\mathbf{p}}_{\mathrm{sys}}=m_{\mathrm{sys}} \overrightarrow{\mathbf{V}}_{\mathrm{cm}} \nonumber \]

We have already determined that the external force is equal to the change of the momentum of the system (Equation (10.4.9)). If we now substitute Equation (10.6.2) into Equation (10.4.9), and continue with our assumption of constant masses \(m_{i}\), we have that

\[\overrightarrow{\mathbf{F}}^{\mathrm{ext}}=\frac{d \overrightarrow{\mathbf{p}}_{\mathrm{sys}}}{d t}=m_{\mathrm{sys}} \frac{d \overrightarrow{\mathbf{V}}_{\mathrm{cm}}}{d t}=m_{\mathrm{sys}} \overrightarrow{\mathbf{A}}_{\mathrm{cm}} \nonumber \]

where \(\overrightarrow{\mathbf{A}}_{\mathrm{cm}}\) the derivative with respect to time of \(\overrightarrow{\mathbf{V}}_{\mathrm{cm}}\) is the acceleration of the center of mass. From Equation (10.6.3) we can conclude that in considering the linear motion of the center of mass, the sum of the external forces may be regarded as acting at the center of mass.

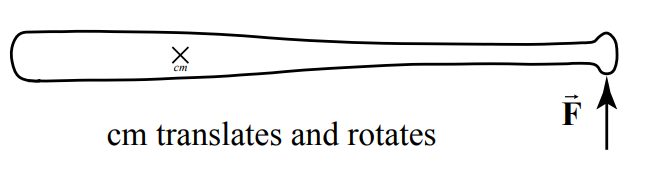
Example 10.4 Forces on a Baseball Bat

Suppose you push a baseball bat lying on a nearly frictionless table at the center of mass, position 2, with a force \(\overrightarrow{\mathbf{F}}\) (Figure 10.7). Will the acceleration of the center of mass be greater than, equal to, or less than if you push the bat with the same force at either end, positions 1 and 3

Figure 10.7 Forces acting on a baseball bat

Solution: The acceleration of the center of mass will be equal in the three cases. From our previous discussion, (Equation (10.6.3)), the acceleration of the center of mass is independent of where the force is applied. However, the bat undergoes a very different motion if we apply the force at one end or at the center of mass. When we apply the force at the center of mass all the particles in the baseball bat will undergo linear motion (Figure 10.7a).

Figure 10.7a Force applied at center of mass

When we push the bat at one end, the particles that make up the baseball bat will no longer undergo a linear motion even though the center of mass undergoes linear motion. In fact, each particle will rotate about the center of mass of the bat while the center of mass of the bat accelerates in the direction of the applied force (Figure 10.7b).

Figure 10.7b Force applied at end of bat