11.2: Galilean Coordinate Transformations

Last updated
Save as PDF

Page ID: 24488

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Let the vector \(\overrightarrow{\mathbf{R}}\) point from the origin of frame \(S\) to the origin of reference frame \(S^{\prime}\). Suppose an object is located at a point 1. Denote the position vector of the object with respect to origin of reference frame \(S\) by \(\overrightarrow{\mathbf{r}}\). Denote the position vector of the object with respect to origin of reference frame \(S^{\prime}\) by \(\overrightarrow{\mathbf{r}}^{\prime}\).

Figure 11.1 Two reference frames \(S\) and S′.

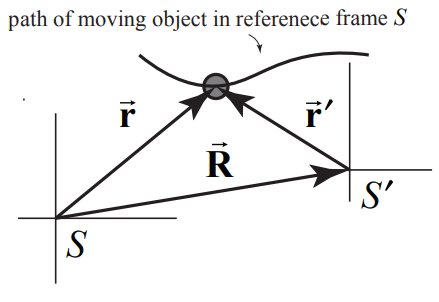
The position vectors are related by

\[\overrightarrow{\mathbf{r}}^{\prime}=\overrightarrow{\mathbf{r}}-\overrightarrow{\mathbf{R}} \nonumber \]

These coordinate transformations are called the Galilean Coordinate Transformations. They enable the observer in frame \(S\) to predict the position vector in frame S′, based only on the position vector in frame \(S\) and the relative position of the origins of the two frames.

The relative velocity between the two reference frames is given by the time derivative of the vector \(\overrightarrow{\mathbf{R}}\), defined as the limit as of the displacement of the two origins divided by an interval of time, as the interval of time becomes infinitesimally small,

\[\overrightarrow{\mathbf{V}}=\frac{d \overrightarrow{\mathbf{R}}}{d t} \nonumber \]

Relatively Inertial Reference Frames and the Principle of Relativity

If the relative velocity between the two reference frames is constant, then the relative acceleration between the two reference frames is zero,

\[\overrightarrow{\mathbf{A}}=\frac{d \overrightarrow{\mathbf{V}}}{d t}=\overrightarrow{\mathbf{0}} \nonumber \]

When two reference frames are moving with a constant velocity relative to each other as above, the reference frames are called relatively inertial reference frames.

We can reinterpret Newton’s First Law

Law 1: Every body continues in its state of rest, or of uniform motion in a right line, unless it is compelled to change that state by forces impressed upon it.

as the Principle of Relativity:

In relatively inertial reference frames, if there is no net force impressed on an object at rest in frame S, then there is also no net force impressed on the object in frame S′ .