12.3: Rocket Propulsion

A rocket at time \(t=t_{i}\) is moving with velocity \(\overrightarrow{\mathbf{V}}_{r, i}\) with respect to a fixed reference frame. During the time interval \(\left[t_{i}, t_{f}\right]\) the rocket continuously burns fuel that is continuously ejected backwards with velocity \(\overrightarrow{\mathbf{u}}\) relative to the rocket. This exhaust velocity is independent of the velocity of the rocket. The rocket must exert a force to accelerate the ejected fuel backwards and therefore by Newton’s Third law, the fuel exerts a force that is equal in magnitude but opposite in direction accelerating the rocket forward. The rocket velocity is a function of time, \(\overrightarrow{\mathbf{v}}_{r}(t)\). Because fuel is leaving the rocket, the mass of the rocket is also a function of time, \(m_{r}(t)\), and is decreasing at a rate \(d m_{r} / d t\). Let \(\overrightarrow{\mathbf{F}}_{e x t}\) denote the total external force acting on the rocket. We shall use the momentum principle, to determine a differential equation that relates \(d \overrightarrow{\mathbf{v}}_{r} / d t\), \(d m_{r} / d t\), \(\overrightarrow{\mathbf{u}}, \overrightarrow{\mathbf{v}}_{r}(t), \text { and } \overrightarrow{\mathbf{F}}_{e x t}\), an equation known as the rocket equation.

We shall apply the momentum principle during the time interval \([t, t+\Delta t]\) with \(\Delta t\) taken to be a small interval (we shall eventually consider the limit that \(\Delta t \rightarrow 0\)), and \(t_{i}<t<t_{f}\) During this interval, choose as our system the mass of the rocket at time t ,

\[m_{s y s}=m_{r}(t)=m_{r, d}+m_{f}(t) \nonumber \]

where \(m_{r, d}\) is the dry mass of the rocket and \(m_{f}(t)\) is the mass of the fuel in the rocket at time t . During the time interval \([t, t+\Delta t]\), a small amount of fuel of mass \(\Delta m_{f}\) (in the limit that \(\Delta t \rightarrow 0, \Delta m_{f} \rightarrow 0\) is ejected backwards with velocity \(\overrightarrow{\mathbf{u}}\) to the rocket. Before the fuel is ejected, it is traveling at the velocity of the rocket and so during the time interval \([t, t+\Delta t]\), the elected fuel undergoes a change in momentum and the rocket recoils forward. At time \(t+\Delta t\) the rocket has velocity \(\overrightarrow{\mathbf{v}}_{r}(t+\Delta t)\). Although the ejected fuel continually changes its velocity, we shall assume that the fuel is all ejected at the instant \(t+\Delta t\) and then consider the limit as \(\Delta t \rightarrow 0\). Therefore the velocity of the ejected fuel with respect to the fixed reference frame is the vector sum of the relative velocity of the fuel with respect to the rocket and the velocity of the rocket, \(\overrightarrow{\mathbf{u}}+\overrightarrow{\mathbf{v}}_{r}(t+\Delta t)\) Figure 12.14 represents momentum diagrams for our system at time t and \(t+\Delta t\) relative to a fixed inertial reference frame in which velocity of the rocket at time t is \(\overrightarrow{\mathbf{v}}_{r}(t)\).

Figure 12.14 Momentum diagrams for system at time t and \(t+\Delta t\)

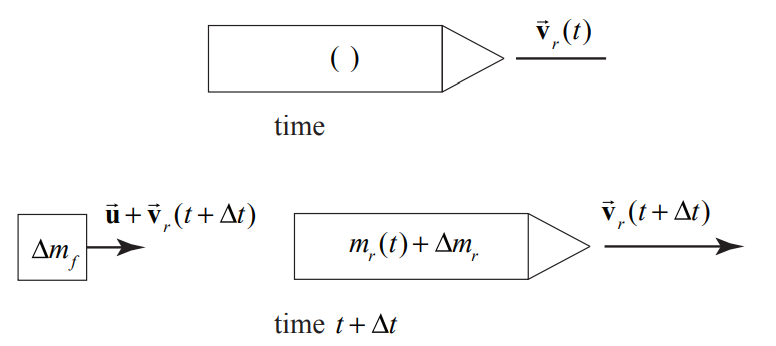
The momentum of the system at time t is

\[\overrightarrow{\mathbf{p}}_{s y s}(t)=m_{r}(t) \overrightarrow{\mathbf{v}}_{r}(t) \nonumber \]

Note that the mass of the system at time t is

\[m_{s y s}=m_{r}(t) \nonumber \]

The momentum of the system at time \(t+\Delta t\) is

\[\overrightarrow{\mathbf{p}}_{s y s}(t+\Delta t)=m_{r}(t+\Delta t) \overrightarrow{\mathbf{v}}_{r}(t+\Delta t)+\Delta m_{f}\left(\overrightarrow{\mathbf{u}}+\overrightarrow{\mathbf{v}}_{r}(t+\Delta t)\right) \nonumber \]

where \(m_{r}(t+\Delta t)=m_{r}(t)+\Delta m_{r}\). With this notation the mass of the system at time \(t+\Delta t\) is given by

\[m_{s y s}=m_{r}(t+\Delta t)+\Delta m_{f}=m_{r}(t)+\Delta m_{r}+\Delta m_{f} \nonumber \]

Because the mass of the system is constant, setting Equation (12.3.69) equal to Equation (12.3.71) requires that

\[\Delta m_{r}=-\Delta m_{f} \nonumber \]

The momentum of the system at time \(t+\Delta t\) (Equation (12.3.70)) can be rewritten as

\[\begin{array}{l}
\overrightarrow{\mathbf{p}}_{s y s}(t+\Delta t)=\left(m_{r}(t)+\Delta m_{r} \overrightarrow{\mathbf{v}}_{r}(t+\Delta t)-\Delta m_{r}\left(\overrightarrow{\mathbf{u}}+\overrightarrow{\mathbf{v}}_{r}(t+\Delta t)\right)\right. \\
\overrightarrow{\mathbf{p}}_{s y s}(t+\Delta t)=m_{r}(t) \overrightarrow{\mathbf{v}}_{r}(t+\Delta t)-\Delta m_{r} \overrightarrow{\mathbf{u}}
\end{array} \nonumber \]

We can now apply Newton’s Second Law in the form of the momentum principle,

\[\begin{array}{l}
\overrightarrow{\mathbf{F}}_{e x t}=\lim _{\Delta t \rightarrow 0} \frac{\left(m_{r}(t) \overrightarrow{\mathbf{v}}_{r}(t+\Delta t)-\Delta m_{r} \overrightarrow{\mathbf{u}}\right)-m_{r}(t) \overrightarrow{\mathbf{v}}_{r}(t)}{\Delta t} \\
=m_{r}(t) \lim _{\Delta t \rightarrow 0} \frac{\overrightarrow{\mathbf{v}}_{r}(t+\Delta t)-\overrightarrow{\mathbf{v}}_{r}(t)}{\Delta t}-\lim _{\Delta t \rightarrow 0} \frac{\Delta m_{r}}{\Delta t} \overrightarrow{\mathbf{u}}
\end{array} \nonumber \]

We now take the limit as

\[\overrightarrow{\mathbf{F}}_{e x t}=m_{r}(t) \frac{d \overrightarrow{\mathbf{v}}_{r}}{d t}-\frac{d m_{r}}{d t} \overrightarrow{\mathbf{u}} \nonumber \]

Equation (12.3.75) is known as the rocket equation.

Suppose the rocket is moving in the positive x -direction with an external force given by \(\overrightarrow{\mathbf{F}}_{e x t}=F_{e x t, x} \hat{\mathbf{i}}\) Then \(\overrightarrow{\mathbf{u}}=-u \hat{\mathbf{i}}\) where u > 0 is the relative speed of the fuel and it is moving in the negative x -direction, \(\overrightarrow{\mathbf{v}}_{r}=v_{r, x} \hat{\mathbf{i}}\) Then the rocket equation (Equation (12.3.75)) becomes

\[F_{e x t, x}=m_{r}(t) \frac{d v_{r, x}}{d t}+\frac{d m_{r}}{d t} u \nonumber \]

Note that the rate of decrease of the mass of the rocket, \(d m_{r} / d t\), is equal to the negative of the rate of increase of the exhaust fuel

\[\frac{d m_{r}}{d t}=-\frac{d m_{f}}{d t} \nonumber \]

We can rewrite Equation (12.3.76) as

\[F_{e x t, x}-\frac{d m_{r}}{d t} u=m_{r}(t) \frac{d v_{r, x}}{d t} \nonumber \]

The second term on the left-hand-side of Equation (12.3.78) is called the thrust

\[F_{t h r u s t, x}=-\frac{d m_{r}}{d t} u=\frac{d m_{f}}{d t} u \nonumber \]

Note that this is not an extra force but the result of the forward recoil due to the ejection of the fuel. Because we are burning fuel at a positive rate \(d m_{f} / d t>0\) and the speed \(u>0\), the direction of the thrust is in the positive x -direction.

Rocket Equation in Gravity-free Space

We shall first consider the case in which there are no external forces acting on the system, then Equation (12.3.78) becomes

\[-\frac{d m_{r}}{d t} u=m_{r}(t) \frac{d v_{r, x}}{d t} \nonumber \]

In order to solve this equation, we separate the variable quantities \(v_{r, x}(t)\) and \(m_{r}(t)\) and multiply both sides by dt yielding

\[d v_{r, x}=-u \frac{d m_{r}}{m_{r}(t)} \nonumber \]

We now integrate both sides of Equation (12.3.81) with limits corresponding to the values of the x -component of the velocity and mass of the rocket at times \(t_{i}\) when the ejection of the burned fuel began and the time \(t_{f}\) when the process stopped,

\[\int_{v_{r, x}^{\prime}=v_{r, x, i}}^{v_{r, x}^{\prime}=v_{r, x, f}} d v_{r, x}^{\prime}=-\int_{m_{r}^{\prime}=m_{r, i}}^{m_{r}^{\prime}=m_{r, f}} \frac{u}{m_{r}^{\prime}} d m_{r}^{\prime} \nonumber \]

Performing the integration and substituting in the values at the endpoints yields

\[v_{r, x, f}-v_{r, x, i}=-u \ln \left(\frac{m_{r, f}}{m_{r, i}}\right) \nonumber \]

Because the rocket is losing fuel, \(m_{r, f}<m_{r, i}\), we can rewrite Equation (12.3.83) as

\[v_{r, x, f}-v_{r, x, i}=u \ln \left(\frac{m_{r, i}}{m_{r, f}}\right) \nonumber \]

We note \(\ln \left(m_{r, i} / m_{r, f}\right)>1\). Therefore \(\boldsymbol{v}_{r, x, f}>\boldsymbol{v}_{r, x, i}\) as we expect. After a slight rearrangement of Equation (12.3.84), we have an expression for the x -component of the velocity of the rocket as a function of the mass \(m_{r}\) of the rocket

\[v_{r, x, f}=v_{r, x, i}+u \ln \left(\frac{m_{r, i}}{m_{r, f}}\right) \nonumber \]

Let’s examine our result. First, let’s suppose that all the fuel was burned and ejected. Then \(m_{r, f} \equiv m_{r, d}\) is the final dry mass of the rocket (empty of fuel). The ratio

\[R=\frac{m_{r, i}}{m_{r, d}} \nonumber \]

is the ratio of the initial mass of the rocket (including the mass of the fuel) to the final dry mass of the rocket (empty of fuel). The final velocity of the rocket is then

\[v_{r, x, f}=v_{r, x, i}+u \ln R \nonumber \]

This is why multistage rockets are used. You need a big container to store the fuel. Once all the fuel is burned in the first stage, the stage is disconnected from the rocket. During the next stage the dry mass of the rocket is much less and so R is larger than the single stage, so the next burn stage will produce a larger final speed then if the same amount of fuel were burned with just one stage (more dry mass of the rocket). In general rockets do not burn fuel at a constant rate but if we assume that the burning rate is constant where

\[b=\frac{d m_{f}}{d t}=-\frac{d m_{r}}{d t} \nonumber \]

then we can integrate Equation (12.3.88)

\[\int_{m^{\prime}=m_{r, i}}^{m_{r}^{\prime}=m_{r}(t)} d m_{r}^{\prime}=-b \int_{t^{\prime}=t_{i}}^{t^{\prime}=t} d t^{\prime} \nonumber \]

and find an equation that describes how the mass of the rocket changes in time

\[m_{r}(t)=m_{r, i}-b\left(t-t_{i}\right) \nonumber \]

For this special case, if we set \(t_{f}=t\) in Equation (12.3.85), then the velocity of the rocket as a function of time is given by

\[v_{r, x, f}=v_{r, x, i}+u \ln \left(\frac{m_{r, i}}{m_{r, i}-b t}\right) \nonumber \]

Example \(\PageIndex{1}\): Single-Stage Rocket

Before a rocket begins to burn fuel, the rocket has a mass of \(m_{r, i}=2.81 \times 10^{7} \mathrm{kg}\), of which the mass of the fuel is \(m_{f, i}=2.46 \times 10^{7} \mathrm{kg}\). The fuel is burned at a constant rate with total burn time is 510 s and ejected at a speed u = 3000 m/s relative to the rocket. If the rocket starts from rest in empty space, what is the final speed of the rocket after all the fuel has been burned?

Solution

The dry mass of the rocket is \(m_{r, d} \equiv m_{r, i}-m_{f, i}=0.35 \times 10^{7} \mathrm{kg}\), hence \(R=m_{r, i} / m_{r, d}=8.03\). The final speed of the rocket after all the fuel has burned is

\[v_{r, f}=\Delta v_{r}=u \ln R=6250 \mathrm{m} / \mathrm{s} \nonumber \]

Example \(\PageIndex{2}\): Two-Stage Rocket

Now suppose that the same rocket in Example 12.4 burns the fuel in two stages ejecting the fuel in each stage at the same relative speed. In stage one, the available fuel to burn is \(m_{f, 1, i}=2.03 \times 10^{7} \mathrm{kg}\) with burn time 150 s . Then the empty fuel tank and accessories from stage one are disconnected from the rest of the rocket. These disconnected parts have a mass \(m=1.4 \times 10^{6} \mathrm{kg}\) All the remaining fuel with mass is burned during the second stage with burn time of 360 s . What is the final speed of the rocket after all the fuel has been burned?

Solution

The mass of the rocket after all the fuel in the first stage is burned is \(m_{r, 1, d}=m_{r, 1, i}-m_{f, 1, i}=0.78 \times 10^{7} \mathrm{kg}\) and \(R_{1}=m_{r, 1, i} / m_{r, 1, d}=3.60\). The change in speed after the first stage is complete is

\[\Delta v_{r, 1}=u \ln R_{1}=3840 \mathrm{m} / \mathrm{s} \nonumber \]

After the empty fuel tank and accessories from stage one are disconnected from the rest of the rocket, the remaining mass of the rocket is \(m_{r, 2, d}=2.1 \times 10^{6} \mathrm{kg}\). The remaining fuel has mass \(m_{f, 2, i}=4.3 \times 10^{6} \mathrm{kg}\). The mass of the rocket plus the unburned fuel at the beginning of the second stage is \(m_{r, 2, i}=6.4 \times 10^{6} \mathrm{kg}\). Then \(R_{2}=m_{r, 2, i} / m_{r, 2, d}=3.05\) Therefore the rocket increases its speed during the second stage by an amount

\[\Delta v_{r, 2}=u \ln R_{2}=3340 \mathrm{m} / \mathrm{s} \nonumber \]

The final speed of the rocket is the sum of the change in speeds due to each stage,

\[v_{f}=\Delta v_{r}=u \ln R_{1}+u \ln R_{2}=u \ln \left(R_{1} R_{2}\right)=7190 \mathrm{m} / \mathrm{s} \nonumber \]

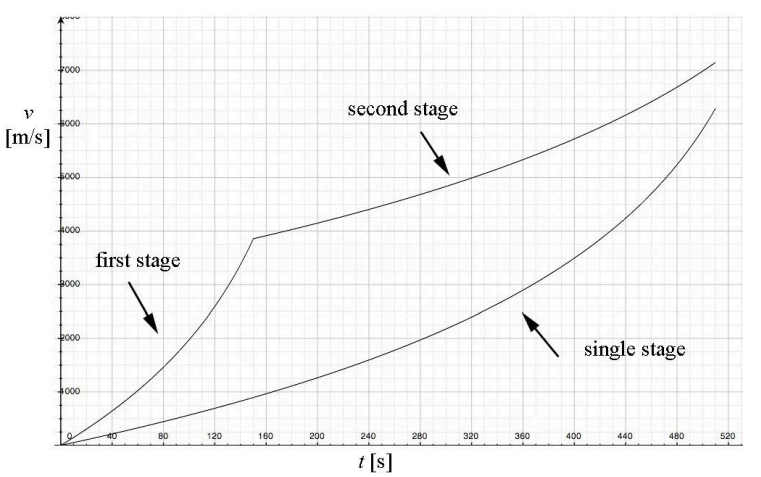
which is greater than if the fuel were burned in one stage. Plots of the speed of the rocket as a function time for both one-stage and two-stage burns are shown Figure 12.15.

Figure 12.15 Plots of speed of rocket for both one-stage burn and two-stage burn

Rocket in a Constant Gravitational Field:

Now suppose that the rocket takes off from rest at time t = 0 in a constant gravitational field then the external force is

\[\overrightarrow{\mathbf{F}}_{\mathrm{ext}}^{\text {total }}=m_{r} \overrightarrow{\mathbf{g}} \nonumber \]

Choose the positive x -axis in the upward direction then \(F_{e x, x}(t)=-m_{r}(t) g\). Then the rocket equation (Equation (12.3.75) becomes

\[-m_{r}(t) g-\frac{d m_{r}}{d t} u=m_{r}(t) \frac{d v_{r, x}}{d t} \nonumber \]

Multiply both sides of Equation (12.3.97) by dt , and divide both sides by \(m_{r}(t)\). Then Equation (12.3.97) can be written as

\[d v_{r, x}=-g d t-\frac{d m_{r}}{m_{r}(t)} u \nonumber \]

We now integrate both sides

\[\int_{v_{r, x,}=0}^{v_{r, x}(t)} d v_{r, x}^{\prime}=-u \int_{m_{r, j}}^{m_{r}(t)} \frac{d m_{r}^{\prime}}{m_{r}^{\prime}}-g \int_{0}^{t} d t^{\prime} \nonumber \]

where \(m_{r, i}\) is the initial mass of the rocket and the fuel. Integration yields

\[v_{r, x}(t)=-u \ln \left(\frac{m_{r}(t)}{m_{r, i}}\right)-g t=u \ln \left(\frac{m_{r, i}}{m_{r}(t)}\right)-g t \nonumber \]

After all the fuel is burned at \(t=t_{f}\), the mass of the rocket is equal to the dry mass \(m_{r, f}=m_{r, d}\) and so

\[v_{r, x}\left(t_{f}\right)=u \ln R-g t_{f} \nonumber \]

The first term on the right hand side is independent of the burn time. However the second term depends on the burn time. The shorter the burn time, the smaller the negative contribution from the third turn, and hence the rocket ends up with a larger final speed. So the rocket engine should burn the fuel as fast as possible in order to obtain the maximum possible speed.