13.12: Appendix 13A Work Done on a System of Two Particles

We shall show that the work done by an internal force in changing a system of two particles of masses \(m_{1}\) and \(m_{1}\) respectively from an initial state A to a final state B is equal to

\[W_{\mathrm{c}}=\frac{1}{2} \mu\left(v_{B}^{2}-v_{A}^{2}\right) \nonumber \]

where \(v_{B}^{2}\) is the square of the relative velocity in state B, \(v_{A}^{2}\) is the square of the relative velocity in state A, and \(\mu=m_{1} m_{2} /\left(m_{1}+m_{2}\right)\).

Consider two bodies 1 and 2 and an interaction pair of forces shown in Figure 13A.1.

Figure 13A.1 System of two bodies interacting

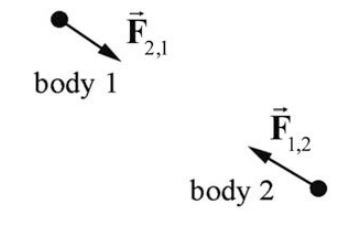
We choose a coordinate system shown in Figure 13A.2.

Figure 13A.2 Coordinate system for two-body interaction

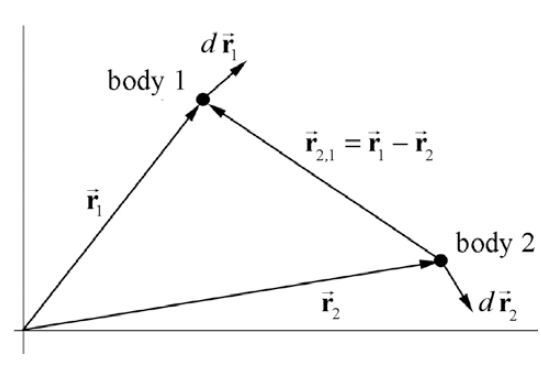
Newton’s Second Law applied to body 1 is

\[\overrightarrow{\mathbf{F}}_{2,1}=m_{1} \frac{d^{2} \overrightarrow{\mathbf{r}}_{1}}{d t^{2}} \nonumber \]

and applied to body 2 is

\[\overrightarrow{\mathbf{F}}_{1,2}=m_{2} \frac{d^{2} \overrightarrow{\mathbf{r}}_{2}}{d t^{2}} \nonumber \]

Divide each side of Equation (13.1.2) by \(m_{1}\),

\[\frac{\overrightarrow{\mathbf{F}}_{2,1}}{m_{1}}=\frac{d^{2} \overrightarrow{\mathbf{r}}_{1}}{d t^{2}} \nonumber \]

and divide each side of Equation (13.1.3) by \(m_{2}\),

\[\frac{\overrightarrow{\mathbf{F}}_{1,2}}{m_{2}}=\frac{d^{2} \overrightarrow{\mathbf{r}}_{2}}{d t^{2}} \nonumber \]

Subtract Equation (13.1.5) from Equation (13.1.4) yielding

\[\frac{\overrightarrow{\mathbf{F}}_{2,1}}{m_{1}}-\frac{\overrightarrow{\mathbf{F}}_{1,2}}{m_{2}}=\frac{d^{2} \overrightarrow{\mathbf{r}}_{1}}{d t^{2}}-\frac{d^{2} \overrightarrow{\mathbf{r}}_{2}}{d t^{2}}=\frac{d^{2} \overrightarrow{\mathbf{r}}_{2,1}}{d t^{2}} \nonumber \]

where \(\overrightarrow{\mathbf{r}}_{2,1}=\overrightarrow{\mathbf{r}}_{1}-\overrightarrow{\mathbf{r}}_{2}\). Use Newton’s Third Law \(\overrightarrow{\mathbf{F}}_{2,1}=-\overrightarrow{\mathbf{F}}_{1,2}\) on the left hand side of Equation (13.1.6) to obtain

\[\overrightarrow{\mathbf{F}}_{2,1}\left(\frac{1}{m_{1}}+\frac{1}{m_{2}}\right)=\frac{d^{2} \overrightarrow{\mathbf{r}}_{1}}{d t^{2}}-\frac{d^{2} \overrightarrow{\mathbf{r}}_{2}}{d t^{2}}=\frac{d^{2} \overrightarrow{\mathbf{r}}_{2,1}}{d t^{2}} \nonumber \]

The quantity \(d^{2} \overrightarrow{\mathbf{r}}_{1,2} / d t^{2}\) is the relative acceleration of body 1 with respect to body 2.

Define

\[\frac{1}{\mu} \equiv \frac{1}{m_{1}}+\frac{1}{m_{2}} \nonumber \]

The quantity \(\mu\) is known as the reduced mass of the system. Equation (13.1.7) now takes the form

\[\overrightarrow{\mathbf{F}}_{2,1}=\mu \frac{d^{2} \overrightarrow{\mathbf{r}}_{2,1}}{d t^{2}} \nonumber \]

The work done in the system in displacing the two masses from an initial state A to a final state B is given by

\[W=\int_{A}^{B} \overrightarrow{\mathbf{F}}_{2,1} \cdot d \overrightarrow{\mathbf{r}}_{1}+\int_{A}^{B} \overrightarrow{\mathbf{F}}_{1,2} \cdot d \overrightarrow{\mathbf{r}}_{2} \nonumber \]

Recall by the work energy theorem that the LHS is the work done on the system,

\[W=\int_{A}^{B} \overrightarrow{\mathbf{F}}_{2,1} \cdot d \overrightarrow{\mathbf{r}}_{1}+\int_{A}^{B} \overrightarrow{\mathbf{F}}_{1,2} \cdot d \overrightarrow{\mathbf{r}}_{2}=\Delta K \nonumber \]

From Newton’s Third Law, the sum in Equation (13.1.10) becomes

\[W=\int_{A}^{B} \overrightarrow{\mathbf{F}}_{2,1} \cdot d \overrightarrow{\mathbf{r}}_{1}-\int_{A}^{B} \overrightarrow{\mathbf{F}}_{2,1} \cdot d \overrightarrow{\mathbf{r}}_{2}=\int_{A}^{B} \overrightarrow{\mathbf{F}}_{2,1} \cdot\left(d \overrightarrow{\mathbf{r}}_{1}-d \overrightarrow{\mathbf{r}}_{2}\right)=\int_{A}^{B} \overrightarrow{\mathbf{F}}_{2,1} \cdot d \overrightarrow{\mathbf{r}}_{2,1} \nonumber \]

where \(d \overrightarrow{\mathbf{r}}_{2,1}\) is the relative displacement of the two bodies. We can now substitute Newton’s Second Law, Equation (13.1.9), for the relative acceleration into Equation (13.1.12),

\[W=\int_{A}^{B} \overrightarrow{\mathbf{F}}_{2,1} \cdot d \overrightarrow{\mathbf{r}}_{2,1}=\int_{A}^{B} \mu \frac{d^{2} \overrightarrow{\mathbf{r}}_{2,1}}{d t^{2}} \cdot d \overrightarrow{\mathbf{r}}_{2,1}=\mu \int_{A}^{B}\left(\frac{d^{2} \overrightarrow{\mathbf{r}}_{2,1}}{d t^{2}} \cdot \frac{d \overrightarrow{\mathbf{r}}_{2,1}}{d t}\right) d t \nonumber \]

where we have used the relation between the differential elements \(d{\mathbf{r}}_{2,1}=\frac{d \overrightarrow{\mathbf{r}}_{2,1}}{d t} d t\). The product rule for derivatives of the scalar product of a vector with itself is given for this case by

\[\frac{1}{2} \frac{d}{d t}\left(\frac{d \overrightarrow{\mathbf{r}}_{2,1}}{d t} \cdot \frac{d \overrightarrow{\mathbf{r}}_{2,1}}{d t}\right)=\frac{d^{2} \overrightarrow{\mathbf{r}}_{2,1}}{d t^{2}} \cdot \frac{d \overrightarrow{\mathbf{r}}_{2,1}}{d t} \nonumber \]

Substitute Equation (13.1.14) into Equation (13.1.13), which then becomes

\[W=\mu \int_{A}^{B} \frac{1}{2} \frac{d}{d t}\left(\frac{d \overrightarrow{\mathbf{r}}_{2,1}}{d t} \cdot \frac{d \overrightarrow{\mathbf{r}}_{2,1}}{d t}\right) d t \nonumber \]

Equation (13.1.15) is now the integral of an exact derivative, yielding

\[W=\left.\frac{1}{2} \mu\left(\frac{d \overrightarrow{\mathbf{r}}_{2,1}}{d t} \cdot \frac{d \overrightarrow{\mathbf{r}}_{2,1}}{d t}\right)\right|_{A} ^{B}=\left.\frac{1}{2} \mu\left(\overrightarrow{\mathbf{v}}_{2,1} \cdot \overrightarrow{\mathbf{v}}_{2,1}\right)\right|_{A} ^{B}=\frac{1}{2} \mu\left(v_{B}^{2}-v_{A}^{2}\right) \nonumber \]

where \(\overrightarrow{\mathbf{V}}_{2,1}\) is the relative velocity between the two bodies. It’s important to note that in the above derivation had we exchanged the roles of body 1 and 2 i.e. \(1 \rightarrow 2 \text { and } 2 \rightarrow 1\) we would have obtained the identical result because

\[\begin{aligned}
\overrightarrow{\mathbf{F}}_{1,2} &=-\overrightarrow{\mathbf{F}}_{2,1} \\
\overrightarrow{\mathbf{r}}_{1,2} &=\overrightarrow{\mathbf{r}}_{2}-\overrightarrow{\mathbf{r}}_{1}=-\overrightarrow{\mathbf{r}}_{2,1} \\
d \overrightarrow{\mathbf{r}}_{1,2} &=d\left(\overrightarrow{\mathbf{r}}_{2}-\overrightarrow{\mathbf{r}}_{1}\right)=-d \overrightarrow{\mathbf{r}} \\
\overrightarrow{\mathbf{v}}_{1,2} &=-\overrightarrow{\mathbf{v}}_{2,1}
\end{aligned} \nonumber \]

Equation (13.1.16) implies that the work done is the change in the kinetic energy of the system, which we can write in terms of the reduced mass and the change in the square of relative speed of the two objects

\[\Delta K=\frac{1}{2} \mu\left(v_{B}^{2}-v_{A}^{2}\right) \nonumber \]