14.2: Conservative and Non-Conservative Forces

Our first type of “energy accounting” involves mechanical energy. There are two types of mechanical energy, kinetic energy and potential energy. Our first task is to define what we mean by the change of the potential energy of a system.

We defined the work done by a force \(\overrightarrow{\mathrm{F}}\), on an object, which moves along a path from an initial position \(\overrightarrow{\mathbf{r}}_{i}\) to a final position \(\overrightarrow{\mathbf{r}}_{f}\), as the integral of the component of the force tangent to the path with respect to the displacement of the point of contact of the force and the object,

\[W=\int_{\text {path }} \overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}} \nonumber \]

Does the work done on the object by the force depend on the path taken by the object?

Figure 14.2 (a) and (b) Two different paths connecting the same initial and final points

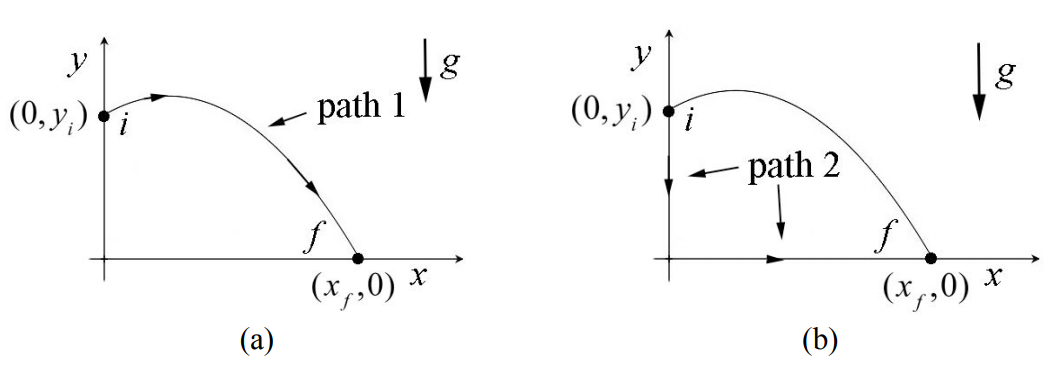
First consider the motion of an object under the influence of a gravitational force near the surface of the earth. Let’s consider two paths 1 and 2 shown in Figure 14.2. Both paths begin at the initial point \(\left(x_{i}, y_{i}\right)=\left(0, y_{i}\right)\) and end at the final point \(\left(x_{f}, y_{f}\right)=\left(x_{f}, 0\right)\). The gravitational force always points downward, so with our choice of coordinates, \(\overrightarrow{\mathbf{F}}=-m g \hat{\mathbf{j}}\). The infinitesimal displacement along path 1 (Figure 14.2a) is given by \(d \overrightarrow{\mathbf{r}}_{1}=d x_{1} \hat{\mathbf{i}}+d y_{1} \hat{\mathbf{j}}\). The scalar product is then

\[\overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}}_{1}=-m g \hat{\mathbf{j}} \cdot\left(d x_{1} \hat{\mathbf{i}}+d y_{1} \hat{\mathbf{j}}\right)=-m g d y_{1} \nonumber \]

The work done by gravity along path 1 is the integral

\[W_{1}=\int_{\text {path } 1} \overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}}=\int_{\left(0, y_{i}\right)}^{\left(x_{f}, 0\right)}-m g d y_{1}=-m g\left(0-y_{i}\right)=m g y_{i} \nonumber \]

Path 2 consists of two legs (Figure 14.2b), leg A goes from the initial point \(\left(0, y_{i}\right)\) to the origin (0,0) , and leg B goes from the origin (0,0) to the final point \(\left(x_{f}, 0\right)\). We shall calculate the work done along the two legs and then sum them up. The infinitesimal displacement along leg A is given by \(d \overrightarrow{\mathbf{r}}_{A}=d y_{A} \hat{\mathbf{j}}\). The scalar product is then

\[\overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}}_{A}=-m g \hat{\mathbf{j}} \cdot d y_{A} \hat{\mathbf{j}}=-m g d y_{A} \nonumber \]

The work done by gravity along leg A is the integral

\[W_{A}=\int_{\operatorname{leg} A} \overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}}_{\mathrm{A}}=\int_{\left(0, y_{i}\right)}^{(0,0)}-m g d y_{A}=-m g\left(0-y_{i}\right)=m g y_{i} \nonumber \]

The infinitesimal displacement along leg B is given by \(d \overrightarrow{\mathbf{r}}_{B}=d x_{B} \hat{\mathbf{i}}\). The scalar product is then

\[\overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}}_{B}=-m g \hat{\mathbf{j}} \cdot d x_{B} \hat{\mathbf{i}}=0 \nonumber \]

Therefore the work done by gravity along leg B is zero, \(W_{B}=0\), which is no surprise because leg B is perpendicular to the direction of the gravitation force. Therefore the work done along path 2 is equal to the work along path 1,

\[W_{2}=W_{A}+W_{B}=m g y_{i}=W_{1} \nonumber \]

Now consider the motion of an object on a surface with a kinetic frictional force between the object and the surface and denote the coefficient of kinetic friction by \(\mu_{\mathrm{k}}\). Let’s compare two paths from an initial point \(x_{i}\) to a final point \(x_{f}\). The first path is a straight-line path. Along this path the work done is just

\[W^{f}=\int_{\text {path } 1} \overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}}=\int_{\mathrm{path} 1} F_{x} d x=-\mu_{\mathrm{k}} N s_{1}=-\mu_{\mathrm{k}} N \Delta x<0 \nonumber \]

where the length of the path is equal to the displacement, \(s_{1}=\Delta x\). Note that the fact that the kinetic frictional force is directed opposite to the displacement, which is reflected in the minus sign in Equation (14.2.8). The second path goes past \(x_{f}\) some distance and them comes back to \(x_{f}\) (Figure 14.3). Because the force of friction always opposes the motion, the work done by friction is negative,

\[W^{f}=\int_{\text {path } 2} \overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}}=\int_{\text {path } 2} F_{x} d x=-\mu_{\mathrm{k}} N s_{2}<0 \nonumber \]

The work depends on the total distance traveled \(s_{2}\), and is greater than the displacement \(s_{2}>\Delta x\). The magnitude of the work done along the second path is greater than the magnitude of the work done along the first path.

Figure 14.3 Two different paths from \(x_{i}\) to \(x_{f}\)

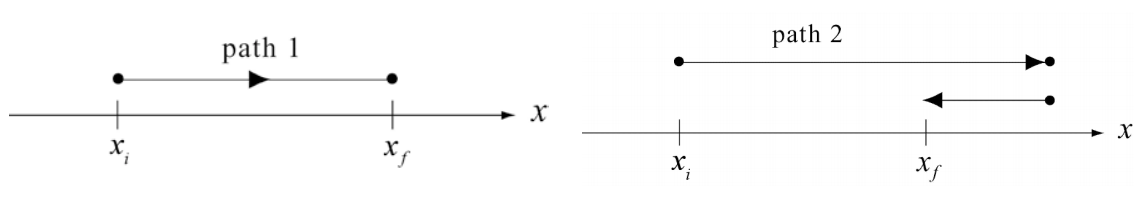
These two examples typify two fundamentally different types of forces and their contribution to work. The work done by the gravitational force near the surface of the earth is independent of the path taken between the initial and final points. In the case of sliding friction, the work done depends on the path taken.

Whenever the work done by a force in moving an object from an initial point to a final point is independent of the path, the force is called a conservative force.

The work done by a conservative force \(\overrightarrow{\mathbf{F}}_{\mathrm{c}}\) in going around a closed path is zero. Consider the two paths shown in Figure 14.4 that form a closed path starting and ending at the point A with Cartesian coordinates (1, 0).

Figure 14.4 Two paths in the presence of a conservative force.

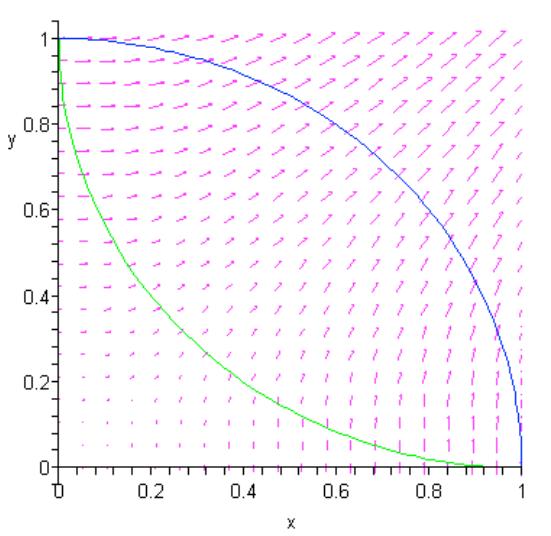
The work done along path 1 (the upper path in the figure, blue if viewed in color) from point A to point B with coordinates (0,1) is given by

\[W_{1}=\int_{A}^{B} \overrightarrow{\mathbf{F}}_{\mathrm{c}}(1) \cdot d \overrightarrow{\mathbf{r}}_{1} \nonumber \]

The work done along path 2 (the lower path, green in color) from B to A is given by

\[W_{2}=\int_{B}^{A} \overrightarrow{\mathbf{F}}_{\mathrm{c}}(2) \cdot d \overrightarrow{\mathbf{r}}_{2} \nonumber \]

The work done around the closed path is just the sum of the work along paths 1 and 2,

\[W=W_{1}+W_{2}=\int_{A}^{B} \overrightarrow{\mathbf{F}}_{\mathrm{c}}(1) \cdot d \overrightarrow{\mathbf{r}}_{1}+\int_{B}^{A} \overrightarrow{\mathbf{F}}_{\mathrm{c}}(2) \cdot d \overrightarrow{\mathbf{r}}_{2} \nonumber \]

If we reverse the endpoints of path 2, then the integral changes sign,

\[W_{2}=\int_{B}^{A} \overrightarrow{\mathbf{F}}_{\mathrm{c}}(2) \cdot d \overrightarrow{\mathbf{r}}_{2}=-\int_{A}^{B} \overrightarrow{\mathbf{F}}_{\mathrm{c}}(2) \cdot d \overrightarrow{\mathbf{r}}_{2} \nonumber \]

We can then substitute Equation (14.2.13) into Equation (14.2.12) to find that the work done around the closed path is

\[W=\int_{A}^{B} \overrightarrow{\mathbf{F}}_{\mathrm{c}}(1) \cdot d \overrightarrow{\mathbf{r}}_{1}-\int_{A}^{B} \overrightarrow{\mathbf{F}}_{\mathrm{c}}(2) \cdot d \overrightarrow{\mathbf{r}}_{2} \nonumber \]

Since the force is conservative, the work done between the points A to B is independent of the path, so

\[\int_{A}^{B} \overrightarrow{\mathbf{F}}_{\mathrm{c}}(1) \cdot d \overrightarrow{\mathbf{r}}_{1}=\int_{A}^{B} \overrightarrow{\mathbf{F}}_{\mathrm{c}}(2) \cdot d \overrightarrow{\mathbf{r}}_{2} \nonumber \]

We now use path independence of work for a conservative force (Equation (14.2.15) in Equation (14.2.14)) to conclude that the work done by a conservative force around a closed path is zero,

\[W=\oint_{\text {closed }} \overrightarrow{\mathbf{F}}_{\mathrm{c}} \cdot d \overrightarrow{\mathbf{r}}=0 \nonumber \]