19.9: External Angular Impulse and Change in Angular Momentum

Define the external angular impulse about a point \(S\) applied as the integral of the external torque about \(S\)

\begin{equation}\overrightarrow{\mathbf{J}}_{S}^{\mathrm{ext}} \equiv \int_{t_{i}}^{t_{f}} \vec{\tau}_{S}^{\mathrm{ext}} d t\end{equation}

Then the external angular impulse about \(S\) is equal to the change in angular momentum

\begin{equation}\overrightarrow{\mathbf{J}}_{S}^{\mathrm{ext}} \equiv \int_{t_{i}}^{t_{f}} \vec{\tau}_{S}^{\mathrm{ext}} d t=\int_{t_{i}}^{t_{f}} \frac{d \overrightarrow{\mathbf{L}}_{S}^{\mathrm{sys}}}{d t} d t=\overrightarrow{\mathbf{L}}_{S, f}^{\mathrm{sys}}-\overrightarrow{\mathbf{L}}_{S, i}^{\mathrm{sys}}\end{equation}

Notice that this is the rotational analog to our statement about impulse and momentum,

\begin{equation}\overrightarrow{\mathbf{I}}_{S}^{\mathrm{ext}} \equiv \int_{t_{i}}^{t_{f}} \overrightarrow{\mathbf{F}}^{\mathrm{ext}} d t=\int_{t_{i}}^{t_{f}} \frac{d \overrightarrow{\mathbf{p}}_{\mathrm{sys}}}{d t} d t=\overrightarrow{\mathbf{p}}_{\mathrm{sys}, f}-\overrightarrow{\mathbf{p}}_{\mathrm{sys}, i}\end{equation}

Example \(\PageIndex{1}\): Angular Impulse on Steel Washer

A steel washer is mounted on the shaft of a small motor. The moment of inertia of the motor and washer is \(I_{0}\). The washer is set into motion. When it reaches an initial angular speed \(\omega_{0}\), at t = 0 , the power to the motor is shut off, and the washer slows down until it reaches an angular speed of \(\omega_{a}\) at time \(t_{a}\). At that instant, a second steel washer with a moment of inertia \(I_{w}\) is dropped on top of the first washer. Assume that the second washer is only in contact with the first washer. The collision takes place over a time \(\Delta t_{\mathrm{int}}=t_{b}-t_{a}\). Assume the frictional torque on the axle is independent of speed, and remains the same when the second washer is dropped. The two washers continue to slow down during the time interval \(\Delta t_{2}=t_{f}-t_{b}\) until they stop at time \(t=t_{f}\). (a) What is the angular acceleration while the washer and motor are slowing down during the interval \(\Delta t_{1}=t_{a}\)? (b) Suppose the collision is nearly instantaneous, \(\Delta t_{\mathrm{int}}=\left(t_{b}-t_{a}\right) \simeq 0\). What is the angular speed \(\omega_{b}\) of the two washers immediately after the collision is finished (when the washers rotate together)?

Figure 19.24 Example 19.8

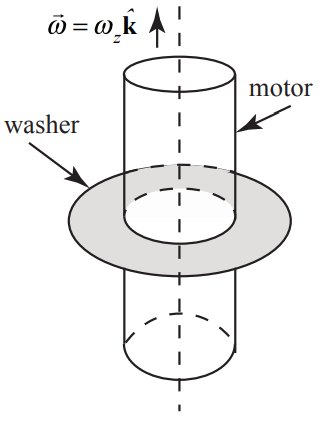
Now suppose the collision is not instantaneous but that the frictional torque is independent of the speed of the rotor. (c) What is the angular impulse during the collision? (d) What is the angular velocity \(\omega_{b}\) of the two washers immediately after the collision is finished (when the washers rotate together)? (e) What is the angular deceleration \(\alpha_{2}\) after the collision?

Solution

a) The angular acceleration of the motor and washer from the instant when the power is shut off until the second washer was dropped is given by

\begin{equation}\alpha_{1}=\frac{\omega_{a}-\omega_{0}}{\Delta t_{1}}<0\end{equation}

(b) If the collision is nearly instantaneous, then there is no angular impulse and therefore the z -component of the angular momentum about the rotation axis of the motor remains constant

\begin{equation}0=\Delta L_{z}=L_{f, z}-L_{0, z}=\left(I_{0}+I_{\mathrm{w}}\right) \omega_{b}-I_{0} \omega_{a}\end{equation}

We can solve Equation (19.5.51) for the angular speed \(\omega_{b}\) of the two washers immediately after the collision is finished

\begin{equation}\omega_{b}=\frac{I_{0}}{I_{0}+I_{\mathrm{w}}} \omega_{a}\end{equation}

(c) The angular acceleration found in part a) is due to the frictional torque in the motor.

Figure 19.25 Frictional torque in the motor

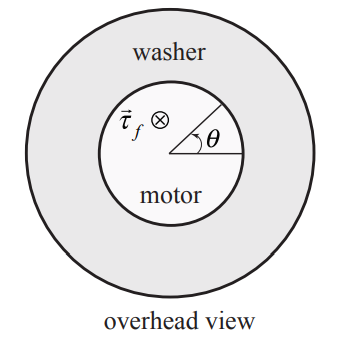
Let \(\vec{\tau}_{f}=-\tau_{f} \hat{\mathbf{k}} \text { where } \tau_{f}\) is the magnitude of the frictional torque (Figure 19.25) then

\begin{equation}-\tau_{f}=I_{0} \alpha_{1}=\frac{I_{0}\left(\omega_{a}-\omega_{0}\right)}{\Delta t_{1}}\end{equation}

During the collision with the second washer, the frictional torque exerts an angular impulse (pointing along the z -axis in the figure),

\begin{equation}J_{z}=-\int_{t_{a}}^{t_{b}} \tau_{f} d t=-\tau_{f} \Delta t_{\mathrm{int}}=I_{0}\left(\omega_{a}-\omega_{0}\right) \frac{\Delta t_{\mathrm{int}}}{\Delta t_{1}}\end{equation}

(d) The z -component of the angular momentum about the rotation axis of the motor changes during the collision,

\begin{equation}\Delta L_{z}=L_{f, z}-L_{0, z}=\left(I_{0}+I_{\mathrm{w}}\right) \omega_{b}-I_{0} \omega_{a}\end{equation}

The change in the z -component of the angular momentum is equal to the z -component of the angular impulse

\begin{equation}J_{z}=\Delta L_{z}\end{equation}

Thus, equating the expressions in Equations (19.5.54) and (19.5.55), yields

\begin{equation}I_{0}\left(\omega_{a}-\omega_{0}\right)\left(\frac{\Delta t_{\text {int }}}{\Delta t_{1}}\right)=\left(I_{0}+I_{\mathrm{w}}\right) \omega_{b}-\left(I_{0}\right) \omega_{a}\end{equation}

Solve Equation (19.5.57) for the angular velocity immediately after the collision,

\begin{equation}\omega_{b}=\frac{I_{0}}{\left(I_{0}+I_{\mathrm{w}}\right)}\left(\left(\omega_{a}-\omega_{0}\right)\left(\frac{\Delta t_{\mathrm{int}}}{\Delta t_{1}}\right)+\omega_{a}\right)\end{equation}

If there were no frictional torque, then the first term in the brackets would vanish, and the second term of Equation (19.5.58) would be the only contribution to the final angular speed.

(e) The final angular acceleration \(\alpha_{2}\) is given by

\begin{equation}\alpha_{2}=\frac{0-\omega_{b}}{\Delta t_{2}}=-\frac{I_{0}}{\left(I_{0}+I_{\mathrm{w}}\right) \Delta t_{2}}\left(\left(\omega_{a}-\omega_{0}\right)\left(\frac{\Delta t_{\mathrm{int}}}{\Delta t_{1}}\right)+\omega_{a}\right)\end{equation}