26.3: Shear Stress and Strain
- Page ID
- 28028
The surface of material may also be subjected to tangential forces producing a shearing action. Consider a block of height h and area A , in which a tangential force, \(\overrightarrow{\mathbf{F}}_{\mathrm{tan}}\) is applied to the upper surface. The lower surface is held fixed. The upper surface will shear by an angle \(\alpha\) corresponding to a horizontal displacement \(\delta x\) The geometry of the shearing action is shown in Figure 26.5.
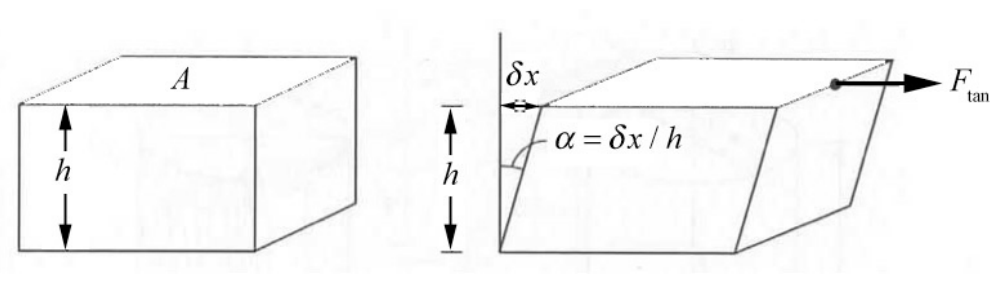
Figure 26.5: Shearing forces
The shear stress is defined to be the ratio of the tangential force to the cross sectional area of the surface upon which it acts,
\begin{equation}\sigma_{S}=\frac{F_{\tan }}{A}\end{equation}
The shear strain is defined to be the ratio of the horizontal displacement to the height of the block,
\begin{equation}\alpha=\frac{\delta x}{h}\end{equation}
For many materials, when the shear stress is sufficiently small, experiment shows that a Hooke’s Law relationship holds in that the shear stress is proportional to shear strain,
\begin{equation}\frac{F_{\text {tan }}}{A}=S \frac{\delta x}{h} \quad \text { (Hooke's Law) }\end{equation}
where the constant of proportional, \(S\), is called the shear modulus. When the deformation angle is small, \(\delta x / h=\tan \alpha \simeq \sin \alpha \simeq \alpha\), and Equation (26.3.3) becomes
\begin{equation}\frac{F_{\text {tan }}}{A} \simeq \(S\) \alpha \quad \text { (Hooke's Law) }\end{equation}
In Table 26.2, the shear modulus is tabulated for various materials.
Table 26.2: Shear Modulus for Various Materials
\begin{equation}\begin{array}{|l|l|}
\hline \text { Material } & \text { Shear Modulus, } \(S\) \text { (Pa) } \\
\hline \text { Nickel } & 7.8 \times 10^{10} \\
\hline \text { Iron } & 7.7 \times 10^{10} \\
\hline \text { Steel } & 7.5 \times 10^{10} \\
\hline \text { Copper } & 4.4 \times 10^{10} \\
\hline \text { Brass } & 3.5 \times 10^{10} \\
\hline \text { Aluminum } & 2.5 \times 10^{10} \\
\hline \text { Crown Glass } & 2.5 \times 10^{10} \\
\hline \text { Lead } & 0.6 \times 10^{10} \\
\hline \text { Rubber } & 2 \times 10^{5}-10 \times 10^{5} \\
\hline
\end{array}\end{equation}
Example 26.1: Stretched wire
An object of mass \(1.5 \times 10^{1} \mathrm{kg}\) is hanging from one end of a steel wire. The wire without the mass has an unstretched length of 0.50 m . What is the resulting strain and elongation of the wire? The cross-sectional area of the wire is \(1.4 \times 10^{-2} \mathrm{cm}^{2}\).
Solution: When the hanging object is attached to the wire, the force at the end of the wire acting on the object exactly balances the gravitational force. Therefore by Newton’s Third Law, the tensile force stressing the wire is
\begin{equation}F_{\perp}=m g\end{equation}
We can calculate the strain on the wire from Hooke’s Law (Equation (26.2.3)) and the value of Young’s modulus for steel \(20 \times 10^{10} \mathrm{Pa} \text { (Table } \left.26.1\right)\).
\begin{equation}\frac{\delta l}{l_{0}}=\frac{F_{\perp}}{Y A}=\frac{m g}{Y A}=\frac{\left(1.5 \times 10^{1} \mathrm{kg}\right)\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)}{\left(2.0 \times 10^{11} \mathrm{Pa}\right)\left(1.4 \times 10^{-6} \mathrm{m}^{2}\right)}=5.3 \times 10^{-4}\end{equation}
The elongation \(\delta l\) of the wire is then
\begin{equation}\delta l=\frac{m g}{Y A} l_{0}=\left(5.3 \times 10^{-4}\right)(0.50 \mathrm{m})=2.6 \times 10^{-4} \mathrm{m}\end{equation}


