17.4: Double Torsion Pendulum
- Page ID
- 7040
Here we have two cylinders of rotational inertias \(I_{1}\) and \(I_{2} \) hanging from two wires of torsion constants \( c_{1}\) and \( c_{2} \).
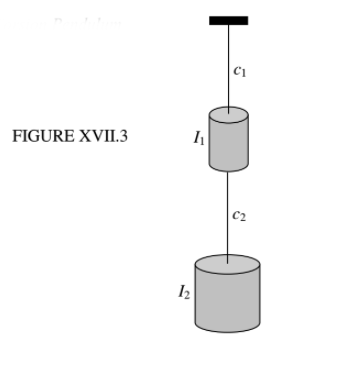
At any instant, the top cylinder is turned through an angle \( \theta_{1} \) from the equilibrium position and the lower cylinder by an angle \( \theta_{2} \) from the equilibrium position (so that, relative to the upper cylinder, it is turned by ). The equations and the description of the motion are just the same as in the previous example, except that \( x_{1}, x_{2}, m_{1}, m_{2}, k_{1}, k_{2} \) are replaced by \( \theta_{1}, \theta_{2}, I_{1}, I_{2}, c_{1}, c_{2} \). The kinetic and potential energies are
\[ T = \frac{1}{2}I_{1}\dot{\theta}_{1}^{2}+ \frac{1}{2}I_{2}\dot{\theta}_{2}^{2}, \label{17.4.1} \]
\[ T = \frac{1}{2}c_{1}{\theta}_{1}^{2}+ \frac{1}{2}c_{2}({\theta}_{2}-{\theta}_{1}) ^{2}. \label{17.4.2} \]
The equations for \( \omega \) and the displacement ratios are just the same, and there is an in-phase and an out-of-phase mode.


