2.11: Plane Laminas. Product Moment. Translation of Axes (Parallel Axes Theorem)
- Page ID
- 8361
We consider a set of point masses distributed in a plane, or a plane lamina. We have hitherto met three second moments of inertia:
\[ A = \sum m_{i}y_{i}^{2}, \label{eq:2.11.1} \]
\[ B = \sum m_{i}x_{i}^{2}, \label{eq:2.11.2} \]
\[ C = \sum m_{i}(x_{i}^{2}+ y_{i}^{2}), \label{eq:2.11.3} \]
These are respectively the moments of inertia about the \(x\)- and \(y\)-axes (assumed to be in the plane of the masses or the lamina) and the \(z\)-axis (normal to the plane). Clearly, \( C = A + B \), which is the perpendicular axes theorem for a plane lamina.
We now introduce another quantity, \(H\), called the product moment of inertia with respect to the \(x\)- and \(y\)-axes, defined by
\[ H = \sum m_{i}x_{i}y_{i} \label{eq:2.11.4} \]
We'll need sometime to ask ourselves whether this has any particular physical significance, or whether it is merely something to calculate for the sake of passing the time of day. In the meantime, the reader should recall the parallel axes theorems (Section 2.5) and, using arguments similar to those given in that section, should derive
\[ H = H_{C}+ M \overline{x} \overline{y} \label{eq:2.11.5} \]
It may also be noted that Equation \( \ref{eq:2.11.4}\) does not contain any squared terms and therefore the product moment of inertia, depending on the distribution of masses, is just as likely to be a negative quantity as a positive one.
We shall defer discussing the physical significance, if any, of the product moment until section \(2.12\). In the meantime let us try to calculate the product moment for a plane right triangular lamina:
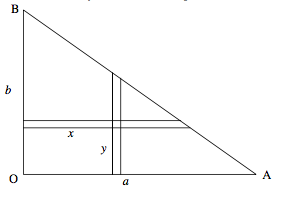
The area of the triangle is \( \frac{1}{2} a b\) and so the mass of the element \( \delta x \delta x\) is \( \frac{2M\delta x \delta y } {ab} \), where \(M\) is the mass of the complete triangle. The product moment of the element with respect to the sides OA, OB is \( \frac{2M x y \delta x \delta y } {ab} \) and so the product moment of the entire triangle is \( \frac{2M}{ab} \int \int xydxdy \). We have to consider carefully the limits of integration. We'll integrate first with respect to \( x \) ; that is to say we integrate along the horizontal (y constant) strip from the side OB to the side AB. That is to say we integrate \( x \delta x \) from where \( x = 0 \) to where \( x = a (1- \frac{y}{b}) \). The product moment is therefore
\[ \dfrac{2M}{ab} \int y \frac{1}{2} a^{2} (1- \frac{y}{b})^{2} dy . \nonumber \]
We now have to add up all the horizontal strips from the side OA, where \( y = 0\), to B, where \(y = b\).
Thus
\[ H = \frac{Ma}{b} \int_{0}^{b} y \left(1- \frac{y}{b}\right)^2 dy, \nonumber \]
which, after some algebra, comes to \( H = \frac {1}{12} Mab \).
The coordinates of the centre of mass with respect to the sides OA, OB are \( \frac{1}{3}a, \frac{1}{3} b \), so that, from Equation \( \ref{eq:2.11.5}\), we find that the product moment with respect to axes parallel to OA, OB and passing through the centre of mass is \( - \frac{1}{36} Mab \).
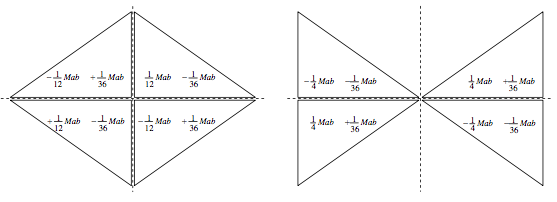
Calculate the product moments of the following eight laminas, each of mass \( M\), with respect to horizontal and vertical axes through the origin, and with respect to horizontal and vertical axes through the centroid of each. (We have just done the first of these, above.) The horizontal base of each is of length \( a\), and the height of each is \(b\). You are going to have to take great care with the signs, and with the limits of integration. If you get an answer right except for the sign, then you have got the answer wrong.
I make the answers as follows.