21.5: Inverse Fourth Power Attractive Force
- Page ID
- 8542
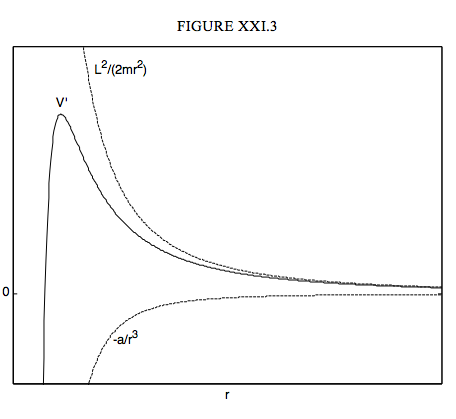
If \( F = -\frac{3a}{r^4} \) then \( V = - \frac{a}{r^3} \), and hence
\[ V' = - \frac{a}{r^3} + \frac{L^2}{2mr^2} \label{eq:21.5.1} \]
I sketch this in Figure XXI.3. The total energy (potential + kinetic) is constant (independent of \(r\)) and is greater than (or equal to) the potential energy. If the total energy is negative, the distance \(r\) has an upper limit, but the only lower limit is the origin, or the centre of attraction, and particle will eventually end there. If the total energy is greater than the maximum of \(V'\), the motion is completely unbounded. If the total energy is positive but less than \(V'_{max}\), the motion depends on the initial value of \(r\). For small \(r\) the motion is bounded above, and the particle will eventually end at the origin. For large \(r\), there is a minimum distance to which the particle can approach the origin, and the particle will eventually wander off to infinity. For total energy in this range, there is a range of \(r\) that is not possible.