6.2: Uniformly Accelerated Motion
- Page ID
- 6961
Before studying motion in a resisting medium, a brief review of uniformly accelerating motion might be in order. That is, motion in which the resistance is zero. Any formulas that we develop for motion in a resisting medium must go to the formulas for uniformly accelerated motion as the resistance approaches zero.
One may imagine a situation in which a body starts with speed \( v_{0}\) and then accelerates at a rate \( a\). One may ask three questions:
How fast is it moving after time \( t\) ?
How far has it moved in time \( t\) ?
How fast is it moving after it has covered a distance \( x\) ?
The answers to these questions are well known to any student of physics:
\[ \ v= v_{0} +at, \tag{6.2.1}\label{eq:6.2.1} \]
\[ \ v= v_{0}t +\frac{1}{2}at^2, \tag{6.2.2}\label{eq:6.2.2} \]
\[ \ v^2= v_{0}^2 +2ax. \tag{6.2.3}\label{eq:6.2.3} \]
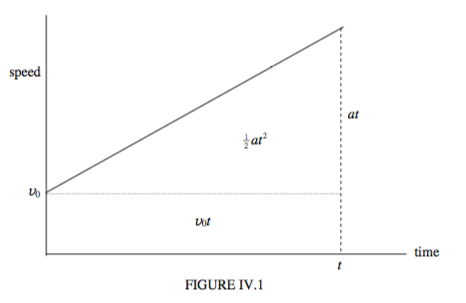
Since the acceleration is uniform, there is no need to use calculus to derive these. The first follows immediately from the meaning of acceleration. Distance travelled is the area under a speed : time graph. Figure VI.1 shows a speed : time graph for constant acceleration, and Equation \( \ref{eq:6.2.2}\) is obvious from a glance at the graph. Equation \( \ref{eq:6.2.3}\) can be obtained by elimination of \( t\) between Equations \( \ref{eq:6.2.1}\) and \( \ref{eq:6.2.2}\). (It can also be deduced from energy considerations, though that is rather putting the cart before the horse.)
Nevertheless, although calculus is not necessary, it is instructive to see how calculus can be used to analyse uniformly accelerated motion, since calculus will be necessary in less simple situations. We shall be using calculus to answer the three questions posed earlier in the section.
For uniformly accelerated motion, the Equation of motion is
\[ \ \ddot{x}=a. \tag{6.2.4}\label{eq:6.2.4} \]
To answer the first question, we write \( \ddot{x}\) as \( \frac{dv}{dt}\), and then the integral (with initial condition \( x=0\) when \( t=0\)) is
\[ \ v = v_{0} + at. \tag{6.2.5}\label{eq:6.2.5} \]
This is the first time integral.
Next, we write \( v\) as \( \frac{dv}{dt}\) and integrate again with respect to time, to get
\[ \ x = v_{0}t + \frac{1}{2}at^2. \tag{6.2.6}\label{eq:6.2.6} \]
This is the second time integral.
To obtain the answer to the third question, which will be called the space integral, we must remember to write \( \ddot{x} \) as \( v \frac{dv}{dt}\). Thus the Equation of motion (Equation \( \ref{eq:6.2.4}\)) is
\[ \ v\frac{dv}{dx}= a. \tag{6.2.7}\label{eq:6.2.7} \]
When this is integrated with respect to \( x\) (with initial condition \( v=v_{0}\) when \( x=0\)) we obtain
\[ \ v^{2} = v^2_{0} +2ax. \tag{6.2.8}\label{eq:6.2.8} \]
This is the space integral.
Examples.
Here are a few quick examples of problems in uniformly accelerated motion. It is probably a good idea to work in algebra and obtain algebraic solutions to each problem. That is, even if you are told that the initial speed is 15 ms-1, call it \(v_{0}\), or, if you are told that the height is 900 feet, call it \( h\). You will probably find it helpful to sketch graphs either of distance versus time or speed versus time in most of the problems. One last little hint: Remember that the two solutions of a quadratic Equation are equal if \( b^{2}=4ac\).
A body is dropped from rest. The last third of the distance before it hits the ground is covered in time T. Show that the time taken for the entire fall to the ground is 5.45T.
The Lady is 8 metres from the bus stop, when the Bus, starting from rest at the bus stop, starts to move off with an acceleration of 0.4 m s-2. What is the least speed at which the Lady must run in order to catch the Bus?
Answer: 2.53ms-1.
A parachutist is descending at a constant speed of 10 feet per second. When she is at a height of 900 feet, her friend, directly below her, throws an apple up to her. What is the least speed at which he must throw the apple in order for it to reach her? How long does it take to reach her, what height is she at then, and what is the relative speed of parachutist and apple? Assume \( g\) = 32 ft s-2. Neglect air resistance for the apple (but not for the parachutist!)
Answer:230fts-1, 7.5s, 825 ft, 0fts-1.
A lunar explorer performs the following experiment on the Moon in order to determine the gravitational acceleration \( g\) there. He tosses a lunar rock upwards at an initial speed of 15 m s-1. Eight seconds later he tosses another rock upwards at an initial speed of 10 m s-1. He observes that the rocks collide 16.32 seconds after the launch of the first rock. Calculate g and also the height of the collision.
Answer: 1.64ms-2, 26.4m
Mr A and Mr B are discussing the merits of their cars. Mr A can go from 0 to 50 mph in ten seconds, and Mr B can go from 0 to 60 mph in 20 seconds. Mr B gives Mr A a start of one second. Assuming that each driver first accelerates uniformly to his maximum speed and thereafter travels at each uniform speed, how long does it take Mr B to catch Mr A, and how far have the cars travelled by then?
Answer: 41 s, half a mile.
I make the answers as follows. Let me know (jtatum@uvic.ca) if you think I have got any of them wrong.


