6.3A: Resistive Force Only
- Page ID
- 8886
It is difficult to imagine a real situation in which the one and only force is a resistive force proportional to the speed. A body falling through the air won't do, because, in addition to the resistive force, there is the acceleration due to gravity. Perhaps we could imagine a puck sliding across the ice. The ice would have to be presumed to be completely frictionless, and the only force on the puck would be the resistance of the air. It is a slightly artificial situation, because we want the puck to be going so fast that the frictional force is negligible compared with the air resistance, but not so fast that the airflow is turbulent - but we need to start somewhere. The frictional force is, at least to a very good approximation, not a function of speed, but is constant, and we shall start by assuming that it is negligible and that the only horizontal force on the puck is air resistance and that the air resistance is proportional to the speed.
In this case, the Equation of motion is indeed Equation 6.3.2. To obtain the first time integral, we write \( \dot{x}\) as \( v\) and the first time integral is readily found to be
\[ v = v_{0}e^{-\gamma t}. \tag{6.3.3}\label{eq:6.3.3} \]
Here \( v_{0}\) is the initial speed. This is illustrated in Figure VI.2
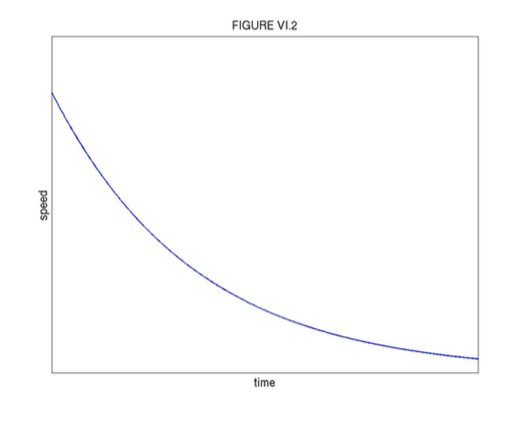
The speed is reduced to half of the initial speed in a time
\[ t_{\frac{1}{2}} = \frac{\ln2}{\gamma} = \frac{0.693}{\gamma}. \tag{6.3.4}\label{eq:6.3.4} \]
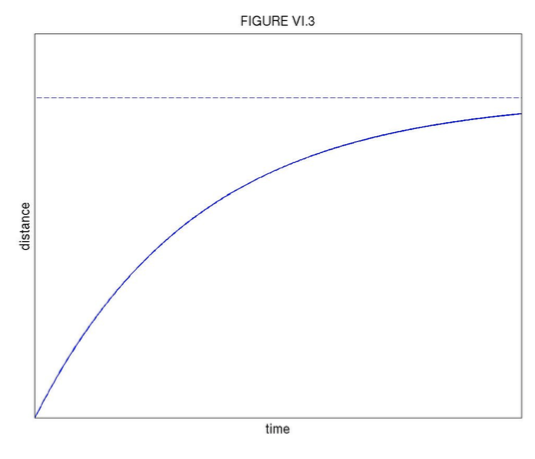
The second time integral is found by writing \( v\) in Equation \( \ref{eq:6.3.3}\) as \( \frac{dx}{dt}\). Integration, with initial condition \( x = 0\) when \( t = 0\), gives
\[ x = x_{∞}(1-e^{-\gamma t}), \tag{6.3.5}\label{eq:6.3.5} \]
where \( x_{\infty}=\frac{v_{0}}{\gamma}\). This is illustrated in Figure VI.3. It is seen that the puck travels an eventual distance of \( x_{\infty}\), but only after an infinite time.
We can obtain the space integral either by eliminating \( t\) from between the two time integrals, or by writing the Equation of motion as
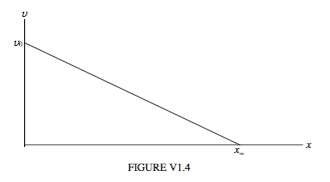
\[ v\frac{dv}{dx} = - \gamma v. \tag{6.3.6}\label{eq:6.3.6} \]
With initial condition \( v = v_{0}\) when \( x = 0\), this becomes
\[ v = v_{0} - \gamma x, \tag{6.3.7}\label{eq:6.3.7} \]
which is illustrated in Figure VI.4. The speed drops linearly with distance (but exponentially with time) reaching zero after having travelled a finite distance \( x_{\infty}=\frac{v_{0}}{\gamma}\) in an infinite time.
This analysis has assumed that the only force was the resistive force proportional to the speed. In the case of our imaginary ice puck, we were assuming that the resistive force was that of the air, the friction being negligible. Of course, as the puck slows down and the resistive force becomes less, there will come a point when the frictional force is no longer negligible compared with the ever-decreasing air resistance, so that the above Equations no longer accurately describe the motion. We shall come back to this point in subsection 3c.


