8.6: Drag Forces in Fluids
- Page ID
- 24471
When a solid object moves through a fluid it will experience a resistive force, called the drag force, opposing its motion. The fluid may be a liquid or a gas. This force is a very complicated force that depends on both the properties of the object and the properties of the fluid. The force depends on the speed, size, and shape of the object. It also depends on the density, viscosity and compressibility of the fluid.
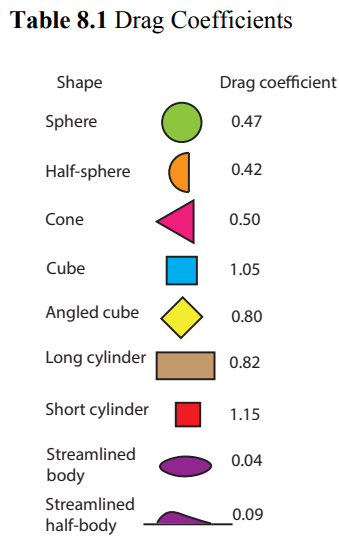
For objects moving in air, the air drag is still quite complicated but for rapidly Table 8.1 Drag Coefficients moving objects the resistive force is roughly proportional to the square of the speed v , the cross-sectional area A of the object in a plane perpendicular to the motion, the density ρ of the air, and independent of the viscosity of the air. Traditional the magnitude of the air drag for rapidly moving objects is written as
\[F_{\mathrm{drag}}=\frac{1}{2} C_{D} A \rho v^{2} \nonumber \]
The coefficient \(C_{D}\) is called the drag coefficient, a dimensionless number that is a property of the object. Table 8.1 lists the drag coefficient for some simple shapes, (each of these objects has a Reynolds number of order 104 ).
The above model for air drag does not extend to all fluids. An object dropped in oil, molasses, honey, or water will fall at different rates due to the different viscosities of the fluid. For very low speeds, the drag force depends linearly on the speed and is also proportional to the viscosity η of the fluid. For the special case of a sphere of radius R , the drag force law can be exactly deduced from the principles of fluid mechanics and is given by
\[\overrightarrow{\mathbf{F}}_{\mathrm{drag}}=-6 \pi \eta R \overrightarrow{\mathbf{v}} \quad(\text { sphere }) \nonumber \]
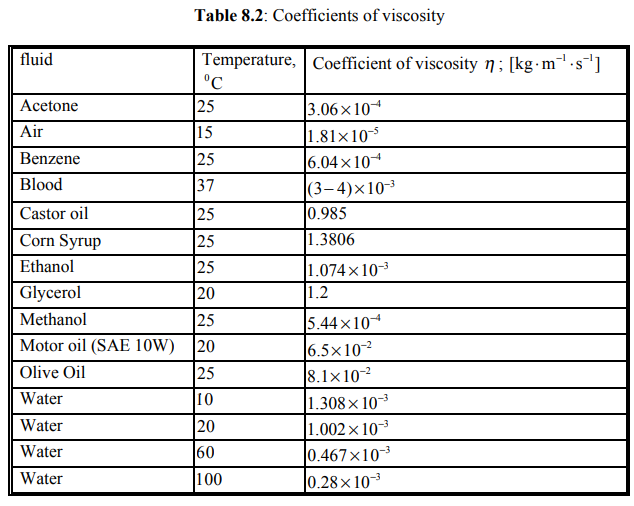
This force law is known as Stokes’ Law. The coefficient of viscosity η has SI units of \(\left[\mathrm{N} \cdot \mathrm{m}^{-2} \cdot \mathrm{s}\right]=[\mathrm{Pa} \cdot \mathrm{s}]=\left[\mathrm{kg} \cdot \mathrm{m}^{-1} \cdot \mathrm{s}^{-1}\right]\); a cgs unit called the poise is often encountered . Some typical coefficients of viscosity are listed in Table 8.2.
This law can be applied to the motion of slow moving objects in a fluid, for example: very small water droplets falling in a gravitational field, grains of sand settling in water, or the sedimentation rate of molecules in a fluid. In the later case, If we model a molecule as a sphere of radius R , the mass of the molecule is proportional to R3 and the drag force is proportion to R , therefore different sized molecules will have different rates of acceleration. This is the basis for the design of measuring devices that separate molecules of different molecular weights.
In many physical situations the force on an object will be modeled as depending on the object’s velocity. We have already seen static and kinetic friction between surfaces modeled as being independent of the surfaces’ relative velocity. Common experience (swimming, throwing a Frisbee) tells us that the frictional force between an object and a fluid can be a complicated function of velocity. Indeed, these complicated relations are an important part of such topics as aircraft design.
Example 8.5 Drag Force at Low Speeds

A spherical marble of radius R and mass m is released from rest and falls under the influence of gravity through a jar of olive oil of viscosity η . The marble is released from rest just below the surface of the olive oil, a height h from the bottom of the jar. The gravitational acceleration is g (Figure 8.31). Neglect any force due to the buoyancy of the olive oil. (i) Determine the velocity of the marble as a function of time, (ii) what is the maximum possible velocity \(\overrightarrow{\mathbf{v}}_{\infty}=\overrightarrow{\mathbf{v}}(t=\infty)\) (terminal velocity), that the marble can obtain, (iii) determine an expression for the viscosity of olive oil η in terms of g , m, R , and \(v_{\infty}=\left|\overrightarrow{\mathbf{v}}_{\alpha}\right|\) (iv) determine an expression for the position of the marble from just below the surface of the olive oil as a function of time.
Solution: Choose positive y -direction downwards with the origin at the initial position of the marble as shown in Figure 8.32(a).
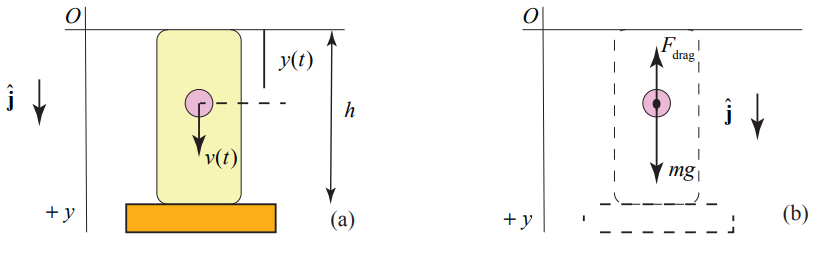
There are two forces acting on the marble: the gravitational force, and the drag force which is given by Equation (8.6.2). The free body diagram is shown in the Figure 8.32(b). Newton’s Second Law is then
\[m g-6 \pi \eta R v=m \frac{d v}{d t} \nonumber \]
where v is the y -component of the velocity of the marble. Let \(\gamma=6 \pi \eta R / m\); the SI units \(\gamma\) are \(\left[\mathrm{S}^{-1}\right]\). Then Equation (8.6.3) becomes
\[g-\gamma v=\frac{d v}{d t} \nonumber \]
Suppose the object has an initial y -component of velocity v(t = 0) = 0 . We shall solve Equation (8.6.3) using the method of separation of variables. The differential equation may be rewritten as
\[\frac{d v}{(v-g / \gamma)}=-\gamma d t \nonumber \]
The integral version of Equation (8.6.5) is then
\[\int_{v^{\prime}=0}^{v^{\prime}=v(t)} \frac{d v^{\prime}}{v^{\prime}-g / \gamma}=-\gamma \int_{t^{\prime}=0}^{t^{\prime}=t} d t^{\prime} \nonumber \]
Integrating both sides of Equation (8.6.6) yields
\[\ln \left(\frac{v(t)-g / \gamma}{-g / \gamma}\right)=-\gamma t \nonumber \]
Recall that \(e^{\ln x}=x\), therefore upon exponentiation of Equation (8.6.7) yields
\[\frac{v(t)-g / \gamma}{-g / \gamma}=e^{-\gamma t} \nonumber \]
Thus the y -component of the velocity as a function of time is given by
\[v(t)=\frac{g}{\gamma}\left(1-e^{-\gamma t}\right)=\frac{m g}{6 \pi \eta R}\left(1-e^{-(6 \pi \eta R / m) t}\right) \nonumber \]
A plot of v(t) vs. t is shown in Figure 8.31 with parameters \(R=5.00 \times 10^{-3} \mathrm{m}\), \(\eta=8.10 \times 10^{-2} \mathrm{kg} \cdot \mathrm{m}^{-1} \cdot \mathrm{s}^{-1}\), \(m=4.08 \times 10^{-3} \mathrm{kg}\), and \(g / \gamma=1.87 \mathrm{m} \cdot \mathrm{s}^{-1}\)

For large values of t , the term \(e^{-(6 \pi \eta R / m) t}\) approaches zero, and the marble reaches a terminal velocity
\[v_{\infty}=v(t=\infty)=\frac{m g}{6 \pi \eta R} \nonumber \]
The coefficient of viscosity can then be determined from the terminal velocity by the condition that
\[\eta=\frac{m g}{6 \pi R v_{t e r}} \nonumber \]
Let \(\rho_{m}\) denote the density of the marble. The mass of the spherical marble is \(m=(4 / 3) \rho_{m} R^{3}\). The terminal velocity is then
\[v_{\infty}=\frac{2 \rho_{m} R^{2} g}{9 \eta} \nonumber \]
The terminal velocity depends on the square of the radius of the marble, indicating that larger marbles will reach faster terminal speeds.
The position of the marble as a function of time is given by the integral expression
\[y(t)-y(t=0)=\int_{t^{\prime}=0}^{t^{\prime}=t} v\left(t^{\prime}\right) d t^{\prime} \nonumber \]
which after substitution of Equation (8.6.9) and integration using the initial condition that y(t = 0) = 0 , becomes
\[y(t)=\frac{g}{\gamma} t+\frac{g}{\gamma^{2}}\left(e^{-\gamma t}-1\right) \nonumber \]
Example 8.6 Drag Forces at High Speeds
An object of mass m at time t = 0 is moving rapidly with velocity \(\overrightarrow{\mathbf{V}}_{0}\) through a fluid of density ρ . Let A denote the cross-sectional area of the object in a plane perpendicular to the motion. The object experiences a retarding drag force whose magnitude is given by Equation (8.6.1). Determine an expression for the velocity of the object as a function of time.
Solution: Choose a coordinate system such that the object is moving in the positive x-direction \(\overrightarrow{\mathbf{v}}=v \hat{\mathbf{i}} . \text { Set } \beta=(1 / 2) C_{D} A \rho\). Newton’s Second Law can then be written as
\[-\beta v^{2}=\frac{d v}{d t} \nonumber \]
An integral version of Equation (8.6.15) is then
\[\int_{v^{\prime}=v_{0}}^{v^{\prime}=v(t)} \frac{d v^{\prime}}{v^{\prime 2}}=-\beta \int_{t^{\prime}=0}^{t^{\prime}=t} d t^{\prime} \nonumber \]
Integration yields
\[-\left(\frac{1}{v(t)}-\frac{1}{v_{0}}\right)=-\beta t \nonumber \]
After some algebraic rearrangement the x -component of the velocity as a function of time is given by
\[v(t)=\frac{v_{0}}{1+v_{0} \beta t}=\frac{1}{1+t / \tau} v_{0} \nonumber \]
where \(\tau=1 / v_{0} \beta\). A plot of v(t) vs. t is shown in Figure 8.34 with initial conditions \(v_{0}=20 \mathrm{m} \cdot \mathrm{s}^{-1}\) and \(\beta=0.5 \mathrm{s}^{-1}\)



