13.10: Worked Examples

Example 13.11 Work Done in a Constant Gravitation Field

The work done in a uniform gravitation field is a fairly straightforward calculation when the body moves in the direction of the field. Suppose the body is moving under the influence of gravity, \(\overrightarrow{\mathbf{F}}=-m g \hat{\mathbf{j}}\) along a parabolic curve. The body begins at the point \(\left(x_{0}, y_{0}\right)\) and ends at the point \(\left(x_{f}, y_{f}\right)\). What is the work done by the gravitation force on the body?

Solution: The infinitesimal line element \(d \overrightarrow{\mathbf{r}}\) is therefore

\[d \overrightarrow{\mathbf{r}}=d x \hat{\mathbf{i}}+d y \hat{\mathbf{j}} \nonumber \]

The scalar product that appears in the line integral can now be calculated,

\[\overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}}=-m g \hat{\mathbf{j}} \cdot[d x \hat{\mathbf{i}}+d y \hat{\mathbf{j}}]=-m g d y \nonumber \]

This result is not surprising since the force is only in the y -direction. Therefore the only non-zero contribution to the work integral is in the y -direction, with the result that

\[W=\int_{\mathrm{r}_{0}}^{\mathrm{r}_{f}} \overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}}=\int_{y=y_{0}}^{y=y_{f}} F_{y} d y=\int_{y=y_{0}}^{y=y_{f}}-m g d y=-m g\left(y_{f}-y_{0}\right) \nonumber \]

In this case of a constant force, the work integral is independent of path.

Example 13.12 Hooke’s Law Spring-Body System

Consider a spring-body system lying on a frictionless horizontal surface with one end of the spring fixed to a wall and the other end attached to a body of mass m (Figure 13.19). Calculate the work done by the spring force on body as the body moves from some initial position to some final position.

Figure 13.19 A spring-body system.

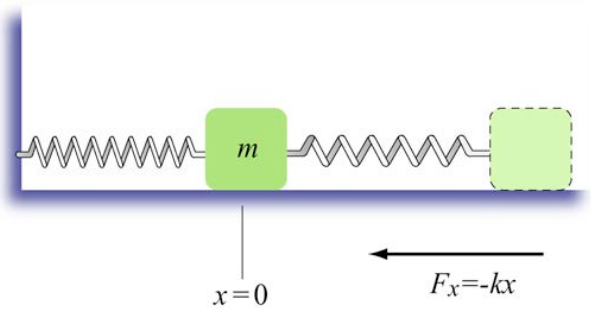
Solution: Choose the origin at the position of the center of the body when the spring is relaxed (the equilibrium position). Let x be the displacement of the body from the origin. We choose the \(+\hat{\mathbf{i}}\) unit vector to point in the direction the body moves when the spring is being stretched (to the right of x = 0 in the figure). The spring force on the body is then given by

\[\overrightarrow{\mathbf{F}}=F_{x} \hat{\mathbf{i}}=-k x \hat{\mathbf{i}} \nonumber \]

The work done by the spring force on the mass is

\[W_{\text {spring }}=\int_{x=x_{0}}^{x=x_{f}}(-k x) d x=-\frac{1}{2} k\left(x_{f}^{2}-x_{0}^{2}\right) \nonumber \]

Example 13.13 Work done by the Inverse Square Gravitation Force

Consider a body of mass m in moving in a fixed orbital plane about the sun. The mass of the sun is \(m_{s}\). How much work does the gravitation interaction between the sun and the body done on the body during this motion?

Solution: Let’s assume that the sun is fixed and choose a polar coordinate system with the origin at the center of the sun. Initially the body is at a distance \(r_{0}\) from the center of the sun. In the final configuration the body has moved to a distance \(r_{f}<r_{0}\) from the center of the sun. The infinitesimal displacement of the body is given by \(d \overrightarrow{\mathbf{r}}=d r \hat{\mathbf{r}}+r d \theta \hat{\mathbf{\theta}}\). The gravitation force between the sun and the body is given by

\[\overrightarrow{\mathbf{F}}_{g r a v}=F_{g r a v} \hat{\mathbf{r}}=-\frac{G m_{s} m}{r^{2}} \hat{\mathbf{r}} \nonumber \]

The infinitesimal work done work done by this gravitation force on the body is given by

\[d W=\overrightarrow{\mathbf{F}}_{g r a v} \cdot d \overrightarrow{\mathbf{r}}=\left(F_{g r a v, r} \hat{\mathbf{r}}\right) \cdot(d r \hat{\mathbf{r}}+r d \theta \hat{\mathbf{\theta}})=F_{g r a v, r} d r \nonumber \]

Therefore the work done on the object as the object moves from \(r_{i}\) to \(r_{f}\) is given by the integral

\[W=\int_{r_{i}}^{r_{f}} \overrightarrow{\mathbf{F}}_{g r a v} \cdot d \overrightarrow{\mathbf{r}}=\int_{r_{i}}^{r_{f}} F_{g r a v, r} d r=\int_{r_{i}}^{r_{f}}\left(-\frac{G m_{\mathrm{sun}} m}{r^{2}}\right) d r \nonumber \]

Upon evaluation of this integral, we have for the work

\[W=\int_{r_{i}}^{r_{f}}\left(-\frac{G m_{\operatorname{sun}} m}{r^{2}}\right) d r=\left.\frac{G m_{\mathrm{sun}} m}{r}\right|_{r_{i}} ^{r_{f}}=G m_{\mathrm{sun}} m\left(\frac{1}{r_{f}}-\frac{1}{r_{i}}\right) \nonumber \]

Because the body has moved closer to the sun, \(r_{f}<r_{i}\), hence \(1 / r_{f}>1 / r_{i}\). Thus the work done by gravitation force between the sun and the body, on the body is positive,

\[W=G m_{\operatorname{sun}} m\left(\frac{1}{r_{f}}-\frac{1}{r_{i}}\right)>0 \nonumber \]

We expect this result because the gravitation force points along the inward radial direction, so the scalar product and hence work of the force and the displacement is positive when the body moves closer to the sun. Also we expect that the sign of the work is the same for a body moving closer to the sun as a body falling towards the earth in a constant gravitation field, as seen in Example 4.7.1 above.

Example 13.14 Work Done by the Inverse Square Electrical Force

Let’s consider two point-like bodies, body 1 and body 2, with charges \(q_{1}\) and \(q_{2}\) respectively interacting via the electric force alone. Body 1 is fixed in place while body 2 is free to move in an orbital plane. How much work does the electric force do on the body 2 during this motion?

Solution: The calculation in nearly identical to the calculation of work done by the gravitational inverse square force in Example 13.13. The most significant difference is that the electric force can be either attractive or repulsive while the gravitation force is always attractive. Once again we choose polar coordinates centered on body 2 in the plane of the orbit. Initially a distance \(r_{0}\) separates the bodies and in the final state a distance \(r_{f}\) separates the bodies. The electric force between the bodies is given by

\[\overrightarrow{\mathbf{F}}_{\mathrm{elec}}=F_{\mathrm{elec}} \hat{\mathbf{r}}=F_{\text {elec}, r} \hat{\mathbf{r}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r^{2}} \hat{\mathbf{r}} \nonumber \]

The work done by this electric force on the body 2 is given by the integral

\[W=\int_{r_{i}}^{r_{f}} \overrightarrow{\mathbf{F}}_{e l e c} \cdot d \overrightarrow{\mathbf{r}}=\int_{r_{i}}^{r_{f}} F_{e l e c, r} d r=\frac{1}{4 \pi \varepsilon_{0}} \int_{r_{i}}^{r_{f}} \frac{q_{1} q_{2}}{r^{2}} d r \nonumber \]

Evaluating this integral, we have for the work done by the electric force

\[W=\int_{r_{i}}^{r_{f}} \frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r^{2}} d r=-\left.\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r^{2}}\right|_{r_{i}} ^{r_{f}}=-\frac{1}{4 \pi \varepsilon_{0}} q_{1} q_{2}\left(\frac{1}{r_{f}}-\frac{1}{r_{i}}\right) \nonumber \]

If the charges have opposite signs, \(q_{1} q_{2}<0\), we expect that the body 2 will move closer to body 1 so \(r_{f}<r_{i}\) and \(1 / r_{f}>1 / r_{i}\). From our result for the work, the work done by electrical force in moving body 2 is positive,

\[W=-\frac{1}{4 \pi \varepsilon_{0}} q_{1} q_{2}\left(\frac{1}{r_{f}}-\frac{1}{r_{i}}\right)>0 \nonumber \]

Once again we see that bodies under the influence of electric forces only will naturally move in the directions in which the force does positive work. If the charges have the same sign, then \(q_{1} q_{2}>0\). They will repel with \(r_{f}>r_{i}\) and \(1 / r_{f}<1 / r_{i}\). Thus the work is once again positive:

\[W=-\frac{1}{4 \pi \varepsilon_{0}} q_{1} q_{2}\left(\frac{1}{r_{f}}-\frac{1}{r_{i}}\right)>0 \nonumber \]