8.1: Hydrostatics

The mechanics of fluids (defined as the materials that cannot keep their geometric form on their own, and include both liquids and gases) is both more simple and more complex than that of the elastic solids, with the simplicity falling squarely to the domain of statics. \({ }^{1}\) Indeed, fluids, by definition, cannot resist static shear deformations. There are two ways to express this fact. First, we can formally take the shear modulus \(\mu\), describing this resistance, to equal zero. Then the Hooke’s law (7.32) shows that the stress tensor is diagonal: \[\sigma_{i j^{\prime}}=\sigma_{j j} \delta_{i j^{\prime}}\] Alternatively, the same conclusion may be reached just by looking at the stress tensor definition (7.19) and/or Figure 7.3, and saying that in the absence of shear stress, the elementary interface \(d \mathbf{F}\) has to be perpendicular to the area element \(d A\), i.e. parallel to the vector \(d \mathbf{A}\).

Moreover, in fluids at equilibrium, all three diagonal components \(\sigma_{i j}\) of the stress tensor have to be equal. To prove that, it is sufficient to single out (mentally rather than physically), from a static fluid, a small volume in the shape of a right prism, with mutually perpendicular faces normal to the two directions we are interested in - in Figure 1, along the \(x\) - and \(y\)-axes.

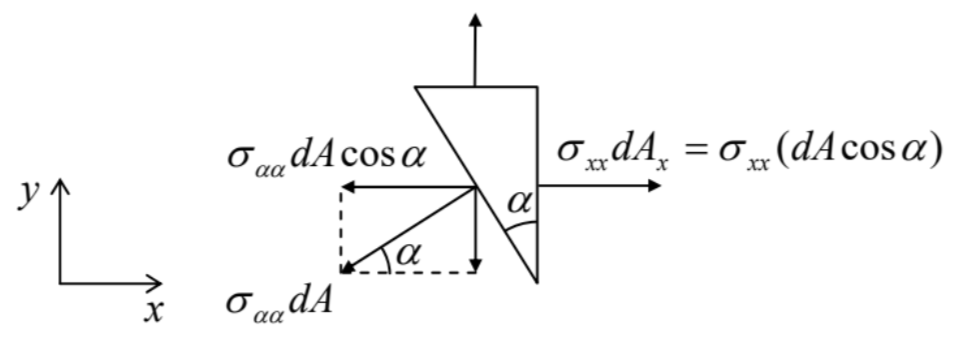Fig. 8.1. Proving the pressure isotropy.

The prism is in equilibrium if each Cartesian component of the vector of the total force exerted on all its faces equals zero. For the \(x\)-component this balance may be expressed as \(\sigma_{x x} d A_{x}-\left(\sigma_{\alpha \alpha} d A\right) \cos \alpha\) \(=0\). However, from the geometry (Figure 1), \(d A_{x}=d A \cos \alpha\), so that the above expression yields \(\sigma_{\alpha \alpha}=\sigma_{x x}\). A similar argument for the \(y\)-component gives \(\sigma_{\alpha \alpha}=\sigma_{y y}\) so that \(\sigma_{x x}=\sigma_{y y}\). Changing the orientation of the prism, we can get such equalities for any pair of diagonal components of the stress tensor, \(\sigma_{j j}\), so that all three of them have to be equal.

This common diagonal element of the stress matrix is usually denoted as \((-\mathcal{P})\), because in the vast majority of cases, the parameter \(\mathcal{P}\), called pressure, is positive. Thus we arrive at the key relation (which has already been mentioned in Sec. 7.2): \[\sigma_{i j^{\prime}}=-\mathcal{P} \delta_{j j^{\prime}}\] In the absence of bulk forces, pressure should be constant through the volume of fluid, due to the translational symmetry. Let us see how this result is affected by bulk forces. With the simple stress tensor (2), the general condition of equilibrium of a continuous medium, expressed by Eq. (7.25) with the left-hand side equal to zero, becomes \[-\frac{\partial \mathcal{P}}{\partial r_{j}}+f_{j}=0,\] and may be re-written in the following convenient vector form: \[-\nabla P+\mathbf{f}=0 .\] In the simplest case of a heavy fluid with mass density \(\rho\), in a uniform gravity field \(\mathbf{f}=\rho \mathbf{g}\), the equation of equilibrium becomes, \[-\nabla \mathcal{P}+\rho \mathbf{g}=0,\] with only one nonzero component (vertical, near the Earth surface). If, in addition, the fluid may be considered incompressible, with its density \(\rho\) constant,\({ }^{2}\) this equation may be readily integrated over the vertical coordinate \((\) say, \(y)\) to give the so-called Pascal equation: \(^{3}\) \[P+\rho g y=\text { const, }\] where the direction of the \(y\)-axis is taken opposite to that of vector \(\mathbf{g}\).

Two manifestations of this key equation are well known. The first one is the fact that in interconnected vessels filled with a fluid, its pressure is equal at all points at the same height \((y)\), regardless of the vessel shape, provided that the fluid is in equilibrium. The second result is the buoyant force \(\mathbf{F}_{\mathrm{b}}\) exerted by a liquid on a (possibly, partly) submerged body, i.e. the vector sum of the elementary pressure forces \(d \mathbf{F}=\mathcal{P} d \mathbf{A}\) exerted on all elementary areas \(d A\) of the submerged part of the body’s surface - see Figure 2. According to Eq. (6), with the constant equal to zero (corresponding to zero pressure at the liquid’s surface taken for \(y=0\), see Figure 2a), the vertical component of this elementary force is \[d F_{y}=d F \cos \varphi=\mathcal{P} d A \cos \varphi=-\rho g y \cos \varphi d A=-\rho g y d A_{h} .\] where \(d A_{h}=\cos \varphi d A\) is the horizontal footprint (say, \(d x d z\) ) of the elementary area \(d A\). Now integrating this relation over all the surface, we get the total vertical buoyant force: 4 \[F_{\mathrm{b}}=\rho g \int_{S}(-y) d A_{h} \equiv \rho g V,\] where \(V\) is the volume of the submerged part of the body’s volume, while \(\rho\) is the liquid’s density, so that by magnitude, \(F_{\mathrm{b}}\) equals the weight of the liquid which would fill the submerged volume.

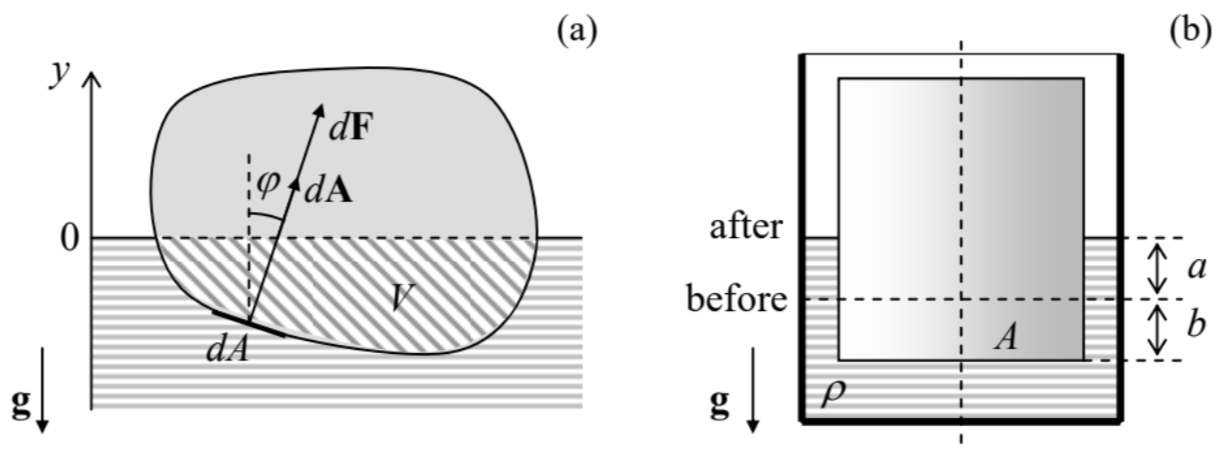Figure 8.2. Calculating the buoyant force.

This well-known Archimedes principle may be proved even more simply using the following argument: the fluid’s pressure forces, and hence the resulting buoyant force, cannot depend on what is inside the body’s volume. Hence \(F_{b}\) would be the same if we filled the volume \(V\) in question with a fluid similar to the surrounding one. But in this case, the surface does not play any role, and the fluid should be still in equilibrium, so that both forces acting on it, the buoyant force \(\mathbf{F}_{\mathrm{b}}\) and the internal liquid’s weight \(m \mathbf{g}=\rho V \mathbf{g}\), have to be equal and opposite, thus proving Eq. (8) again.

Despite the simplicity of the Archimedes principle, its different, erroneous formulations, such as "The buoyant force’s magnitude is equal to the weight of the displaced liquid" [WRONG!] creep from one undergraduate textbook to another, leading to application errors. A typical example is shown in Figure \(2 \mathrm{~b}\), where a solid vertical cylinder with the base area \(A\) is pressed into a liquid inside a container of comparable size, pushing the liquid’s level up. The correct answer for the buoyant force, following from Eq. (8), is \[F_{\mathrm{b}}=\rho g V=\rho g A(a+b),\] because the volume \(V\) of the submerged part of the cylinder is evidently \(A(a+b)\). But the wrong formulation cited above, using the term displaced liquid, would give a different answer: \[F_{\mathrm{b}}=\rho g V_{\text {displaced }}=\rho g A b . \quad[\text { WRONG! }]\] (The latter result is correct only asymptotically, in the limit of a very large container.)

Another frequent error in hydrostatics concerns the angular stability of a freely floating body the problem evidently of vital importance for the boat/ship design. It is sometimes claimed that the body is stable only if the so-called buoyancy center, the effective point of buoyant force application (in Fig, 3 , point \(\mathrm{B})\), is above the center of mass \((0)\) of the whole floating body. \({ }^{5}\) However, as Figure 3 shows, this is unnecessary; indeed in the shown case, point B (which is just the center of mass the liquid would have in the submerged part) is below point 0 , even at a small tilt. Still, in this case, the torque created by the pair of forces \(\mathbf{F}_{\mathrm{b}}\) and \(m \mathbf{g}\) tries to return the body to the equilibrium position, which is therefore stable. As Figure 3 shows, the actual condition of the angular stability may be expressed as the requirement for point M (in shipbuilding, called the metacenter of the ship’s hull) to be above the ship’s center of mass \(0 .{ }^{6}\)

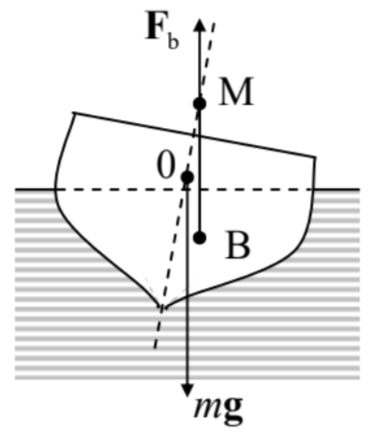Figure 8.3. Angular stability of a floating body.

To conclude this section, let me note that the integration of Eq. (4) may be more complex in the case if the bulk forces \(\mathbf{f}\) depend on position, \({ }^{7}\) and/or if the fluid is substantially compressible. In the latter case, Eq. (4) has to be solved together with the medium-specific equation of state \(\rho=\rho(\mathcal{P})\) describing its compressibility law - whose example is given by Eq. (7.38) for ideal gases: \(\rho \equiv m N / V=\) \(m \mathcal{P} / k_{\mathrm{B}} T\), where \(m\) is the mass of one gas molecule.

---

\({ }^{1}\) It is often called hydrostatics because water has always been the most important liquid for the human race and hence for science and engineering.

\({ }^{2}\) As was discussed in Sec. \(7.3\) in the context of Table 7.1, this is an excellent approximation, for example, for human-scale experiments with water.

\({ }^{3}\) The equation, and the SI unit of pressure \(1 \mathrm{~Pa} \equiv 1 \mathrm{~N} / \mathrm{m}^{2}\), are named after Blaise Pascal (1623-1662) who has not only pioneered hydrostatics, but also invented the first mechanical calculator, and made several other important contributions to mathematics - and to Christian philosophy!

\({ }^{4}\) The force is strictly vertical, because the horizontal components of the elementary forces \(d \mathbf{F}\) exerted on opposite elementary areas \(d A\), at the same height \(y\), cancel.

\({ }^{5}\) Please note the crucial difference between the whole body and that of its submerged part.

\({ }^{6}\) A small tilt of the body leads to a small lateral displacement of point B, but does not affect the position of the metacenter M.

\({ }^{7}\) A simple example of such a problem is given by the fluid equilibrium in a container rotating with a constant angular velocity \(\omega\). If we solve such a problem in a reference frame rotating together with the container, the real bulk forces should be complemented by the centrifugal "force" (4.93), depending on \(\mathbf{r}\).