30.9: The Pauli Exclusion Principle
- Page ID
- 2774
Learning Objectives
By the end of this section, you will be able to:
- Define the composition of an atom along with its electrons, neutrons, and protons.
- Explain the Pauli exclusion principle and its application to the atom.
- Specify the shell and subshell symbols and their positions.
- Define the position of electrons in different shells of an atom.
- State the position of each element in the periodic table according to shell filling.
Multiple-Electron Atoms
All atoms except hydrogen are multiple-electron atoms. The physical and chemical properties of elements are directly related to the number of electrons a neutral atom has. The periodic table of the elements groups elements with similar properties into columns. This systematic organization is related to the number of electrons in a neutral atom, called the atomic number, \(Z\). We shall see in this section that the exclusion principle is key to the underlying explanations, and that it applies far beyond the realm of atomic physics.
In 1925, the Austrian physicist Wolfgang Pauli (see Figure) proposed the following rule: No two electrons can have the same set of quantum numbers. That is, no two electrons can be in the same state. This statement is known as the Pauli exclusion principle, because it excludes electrons from being in the same state. The Pauli exclusion principle is extremely powerful and very broadly applicable. It applies to any identical particles with half-integral intrinsic spin—that is, having \(s = 1/2, \, 3/2, . . .\) Thus no two electrons can have the same set of quantum numbers.
Pauli Exclusion Principle
No two electrons can have the same set of quantum numbers. That is, no two electrons can be in the same state.

Let us examine how the exclusion principle applies to electrons in atoms. The quantum numbers involved were defined in Quantum Numbers and Rules as \(n, \, l, \, m_l, \, s\) and \(m_s\). Since \(s\) is always \(1/2\) for electrons, it is redundant to list \(s\), and so we omit it and specify the state of an electron by a set of four numbers \((n, \, l, \, m_l, \, m_s)\). For example, the quantum numbers \((2, \, 1, \, 0, - 1/2)\) completely specify the state of an electron in an atom.
Since no two electrons can have the same set of quantum numbers, there are limits to how many of them can be in the same energy state. Note that \(n\) determines the energy state in the absence of a magnetic field. So we first choose \(n\), and then we see how many electrons can be in this energy state or energy level. Consider the \(n = 1\) level, for example. The only value \(l\) can have is 0 (see [link] for a list of possible values once \(n\) is known), and thus \(m_l\) can only be 0. The spin projection \(m_s\) can be either \(+1/2\) or \(-1/2\), and so there can be two electrons in the \(n = 1\) state. One has quantum numbers \((1,\space 0, \, 0, \, +1/2)\), and the other has \((1, \, 0, \, 0, \, -1/2)\). Figure illustrates that there can be one or two electrons having \(n = 1\), but not three.
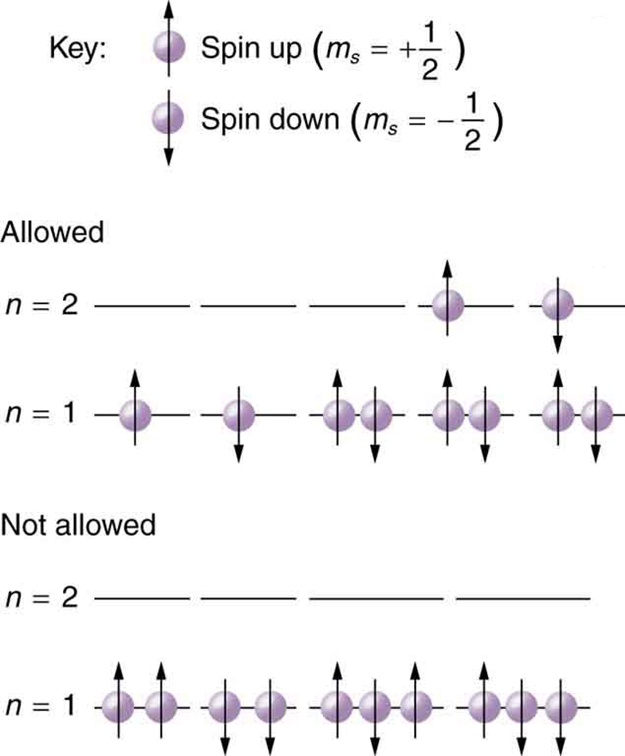
Shells and Subshells
Because of the Pauli exclusion principle, only hydrogen and helium can have all of their electrons in the \(n = 1\) state. Lithium (see the periodic table) has three electrons, and so one must be in the \(n = 2\) level. This leads to the concept of shells and shell filling. As we progress up in the number of electrons, we go from hydrogen to helium, lithium, beryllium, boron, and so on, and we see that there are limits to the number of electrons for each value of \(n\). Higher values of the shell \(n\) correspond to higher energies, and they can allow more electrons because of the various combinations of \(l, \, m_l\), and \(m_s\) that are possible. Each value of the principal quantum number \(n\) thus corresponds to an atomic shell into which a limited number of electrons can go. Shells and the number of electrons in them determine the physical and chemical properties of atoms, since it is the outermost electrons that interact most with anything outside the atom.
The probability clouds of electrons with the lowest value of \(l\) are closest to the nucleus and, thus, more tightly bound. Thus when shells fill, they start with \(l = 0\), progress to \(l = 1\), and so on. Each value of \(l\) thus corresponds to a subshell.
The table given below lists symbols traditionally used to denote shells and subshells.
| Shell | Subshell | Symbol |
|---|---|---|
| \(n\) | \(l\) | |
| 1 | 0 | \(s\) |
| 2 | 1 | \(p\) |
| 3 | 2 | \(d\) |
| 4 | 3 | \(f\) |
| 5 | 4 | \(g\) |
| 6 | \(h\) | |
| \(6^i\) | \(i\) |
To denote shells and subshells, we write \(nl\) with a number for \(n\) and a letter for \(l\). For example, an electron in the \(n = 1\) state must have \(l = 0\) and it is denoted as a \(1s\) electron. Two electrons in the \(n = 1\) state is denoted as \(1s^2\). Another example is an electron in the \(n = 2\) state with \(l = 1\), written as \(2p\).The case of three electrons with these quantum numbers is written \(2p^3\). This notation, called spectroscopic notation, is generalized as shown in Figure.
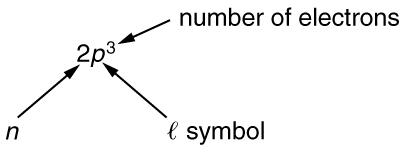
Counting the number of possible combinations of quantum numbers allowed by the exclusion principle, we can determine how many electrons it takes to fill each subshell and shell.
Example \(\PageIndex{1}\): How Many Electrons Can Be in This Shell?
List all the possible sets of quantum numbers for the \(n = 2\) shell, and determine the number of electrons that can be in the shell and each of its subshells.
Strategy
Given \(n = 2\) for the shell, the rules for quantum numbers limit \(l\) to be 0 or 1. The shell therefore has two subshells, labeled \(2s\) and \(2p\). Since the lowest \(l\) subshell fills first, we start with the \(2s\) subshell possibilities and then proceed with the \(2p\) subshell.
Solution
It is convenient to list the possible quantum numbers in a table, as shown below.
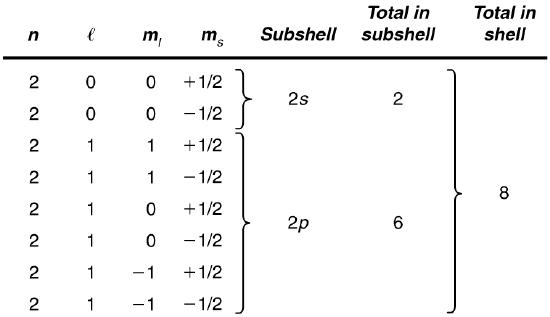
Discussion
It is laborious to make a table like this every time we want to know how many electrons can be in a shell or subshell. There exist general rules that are easy to apply, as we shall now see.
The number of electrons that can be in a subshell depends entirely on the value of \(l\). Once \(l\) is known, there are a fixed number of values of \(m_l\), each of which can have two values for \(m_s\). First, since \(m_l\) goes from \(-l\) to \(l\) in steps of 1, there are \(2l + 1\) possibilities. This number is multiplied by 2, since each electron can be spin up or spin down. Thus the maximum number of electrons that can be in a subshell is \(2(2l + 1)\).
For example, the \(2s\) subshell in Example has a maximum of 2 electrons in it, since \(2(2l + 1) = 2(0 + 1) = 2\) for this subshell. Similarly, the \(2p\) subshell has a maximum of 6 electrons, since \(2(2l + 1) = 2(2 + 1) = 6\). For a shell, the maximum number is the sum of what can fit in the subshells. Some algebra shows that the maximum number of electrons that can be in a shell is \(2n^2\).
For example, for the first shell \(n = 1\), and so \(2n^2 = 2\). We have already seen that only two electrons can be in the \(n = 1\) shell. Similarly, for the second shell, \(n = 2\), and so \(2n^2 = 8\). As found in Example, the total number of electrons in the \(n = 2\) shell is 8.
Example \(\PageIndex{2}\): Subshells and Totals for \(n = 3\)
How many subshells are in the \(n = 3\) shell? Identify each subshell, calculate the maximum number of electrons that will fit into each, and verify that the total is \(2n^2\).
Strategy
Subshells are determined by the value of \(l\); thus, we first determine which values of \(l\) are allowed, and then we apply the equation “maximum number of electrons that can be in a subshell \(= 2(2l + 1)\)" to find the number of electrons in each subshell.
Solution
Since \(n = 3\), we know that \(l\) can be \(0,\space 1\) or \(2\), thus, there are three possible subshells. In standard notation, they are labeled the \(3s, \, 3p,\) and \(3d\) subshells. We have already seen that 2 electrons can be in an \(s\) state, and 6 in a \(p\) state, but let us use the equation “maximum number of electrons that can be in a subshell \(= 2(2l + 1)\)" to calculate the maximum number in each:
\[3s \, has \, l = 0; \, thus, \, 2(2l + 1) = 2(0 + 1) = 2\]
\[3p \, has \, l = 1; \, thus, \, 2(2l + 1) = 2(2 + 1) = 6\]
\[3d \, has \, l = 2; \, thus, \, 2(2l + 1) = 2(4 + 1) = 10\]
\[Total = 18\]
\[(in \, the \, n = 3 \, shell)\]
The equation “maximum number of electrons that can be in a shell \(= 2n^2\)" gives the maximum number in the \(n = 3\) shell to be
\[Maximum \, number \, of \, electrons = 2n^2 = 2(3)^2 = 2(9) = 18.\]
Discussion
The total number of electrons in the three possible subshells is thus the same as the formula \(2n^2\). In standard (spectroscopic) notation, a filled \(n = 3\) shell is denoted as \(3s^2 3p^6 3d^10\). Shells do not fill in a simple manner. Before the \(n = 3\) shell is completely filled, for example, we begin to find electrons in the \(n = 4\) shell.
Shell Filling and the Periodic Table
Table shows electron configurations for the first 20 elements in the periodic table, starting with hydrogen and its single electron and ending with calcium. The Pauli exclusion principle determines the maximum number of electrons allowed in each shell and subshell. But the order in which the shells and subshells are filled is complicated because of the large numbers of interactions between electrons.
| Element | Number of electrons (Z) | Ground state configuration |
|---|---|---|
| H | 1 | \(1s^1\) |
| He | 2 | \(1s^2\) |
| Li | 3 | \(1s^2 \, 2s^1\) |
| Be | 4 | \( " \, 2s^2\) |
| B | 5 | \( " \, 2s^2 \, 2p^1\) |
| C | 6 | \( " \, 2s^2 \, 2p^2\) |
| N | 7 | \( " \, 2s^2 \, 2p^3\) |
| O | 8 | \( " \, 2s^2 \, 2p^4\) |
| F | 9 | \( " \, 2s^2 \, 2p^5\) |
| Ne | 10 | \( " \, 2s^2 \, 2p^6\) |
| Na | 11 | \( " \, 2s^2 \, 2p^6 \, 3s^1\) |
| Mg | 12 | \( " \, " \, " \, 3s^2\) |
| Al | 13 | \( " \, " \, " \, 3s^2 \, 3p^1\) |
| Si | 14 | \( " \, " \space" \, 3s^2 \, 3p^2\) |
| P | 15 | \( " \space " \, " \, 3s^2 \, 3p^3\) |
| S | 16 | \( " \, " \, " \, 3s^2 \, 3p^4\) |
| Cl | 17 | \( " \, " \, " \, 3s^2 \, 3p^5\) |
| Ar | 18 | \( " \, " \, " \, 3s^2 \, 3p^6\) |
| K | 19 | \( " \, " \, " \, 3s^2 \, 3p^6 \, 4s^1\) |
| Ca | 20 | \( " \, " \, " \, " \, " \, 4s^2\) |
Examining the above table, you can see that as the number of electrons in an atom increases from 1 in hydrogen to 2 in helium and so on, the lowest-energy shell gets filled first—that is, the \(n = 1\) shell fills first, and then the \(n = 2\) shell begins to fill. Within a shell, the subshells fill starting with the lowest \(l\), or with the \(s\) subshell, then the \(p\), and so on, usually until all subshells are filled. The first exception to this occurs for potassium, where the \(4s\) subshell begins to fill before any electrons go into the \(3d\) subshell. The next exception is not shown in Table; it occurs for rubidium, where the \(5s\) subshell starts to fill before the \(4d\) subshell. The reason for these exceptions is that \(l = 0\) electrons have probability clouds that penetrate closer to the nucleus and, thus, are more tightly bound (lower in energy).
Figure shows the periodic table of the elements, through element 118. Of special interest are elements in the main groups, namely, those in the columns numbered 1, 2, 13, 14, 15, 16, 17, and 18.
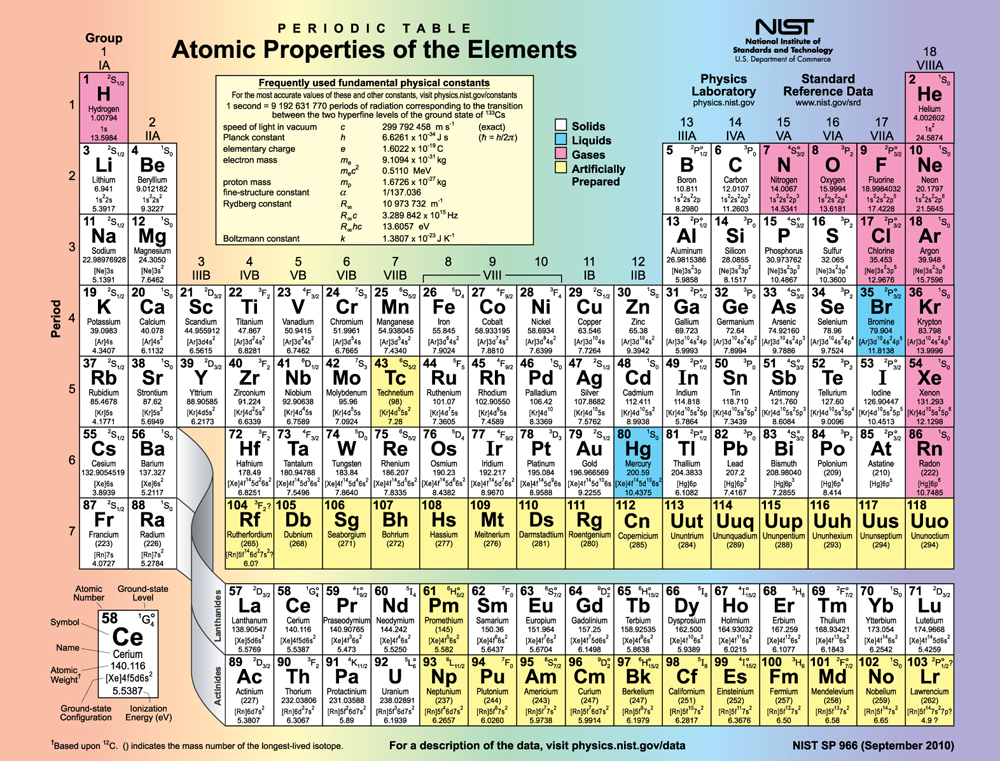
The number of electrons in the outermost subshell determines the atom’s chemical properties, since it is these electrons that are farthest from the nucleus and thus interact most with other atoms. If the outermost subshell can accept or give up an electron easily, then the atom will be highly reactive chemically. Each group in the periodic table is characterized by its outermost electron configuration. Perhaps the most familiar is Group 18 (Group VIII), the noble gases (helium, neon, argon, etc.). These gases are all characterized by a filled outer subshell that is particularly stable. This means that they have large ionization energies and do not readily give up an electron. Furthermore, if they were to accept an extra electron, it would be in a significantly higher level and thus loosely bound. Chemical reactions often involve sharing electrons. Noble gases can be forced into unstable chemical compounds only under high pressure and temperature.
Group 17 (Group VII) contains the halogens, such as fluorine, chlorine, iodine and bromine, each of which has one less electron than a neighboring noble gas. Each halogen has 5\(p\) electrons (a \(p^5\) configuration), while the \(p\) subshell can hold 6 electrons. This means the halogens have one vacancy in their outermost subshell. They thus readily accept an extra electron (it becomes tightly bound, closing the shell as in noble gases) and are highly reactive chemically. The halogens are also likely to form singly negative ions, such as \(Cl^-\) fitting an extra electron into the vacancy in the outer subshell. In contrast, alkali metals, such as sodium and potassium, all have a single \(s\) electron in their outermost subshell (an \(s^1\) configuration) and are members of Group 1 (Group I). These elements easily give up their extra electron and are thus highly reactive chemically. As you might expect, they also tend to form singly positive ions, such as \(Na^+\), by losing their loosely bound outermost electron. They are metals (conductors), because the loosely bound outer electron can move freely.
Of course, other groups are also of interest. Carbon, silicon, and germanium, for example, have similar chemistries and are in Group 4 (Group IV). Carbon, in particular, is extraordinary in its ability to form many types of bonds and to be part of long chains, such as inorganic molecules. The large group of what are called transitional elements is characterized by the filling of the \(d\) subshells and crossing of energy levels. Heavier groups, such as the lanthanide series, are more complex—their shells do not fill in simple order. But the groups recognized by chemists such as Mendeleev have an explanation in the substructure of atoms.
PHET EXPLORATIONS: BUILD AN ATOM
Build an atom out of protons, neutrons, and electrons, and see how the element, charge, and mass change. Then play a game to test your ideas!

Summary
- The state of a system is completely described by a complete set of quantum numbers. This set is written as \((n, \, l, \, m_i, \, m_s)\).
- The Pauli exclusion principle says that no two electrons can have the same set of quantum numbers; that is, no two electrons can be in the same state.
- This exclusion limits the number of electrons in atomic shells and subshells. Each value of \(n\) corresponds to a shell, and each value of \(l\) corresponds to a subshell.
- The maximum number of electrons that can be in a subshell is \(2(2l + 1)\).
- The maximum number of electrons that can be in a shell is \(2n^2\).
Footnotes
- 1 It is unusual to deal with subshells having \(l\) greater than 6, but when encountered, they continue to be labeled in alphabetical order.
Glossary
- atomic number
- the number of protons in the nucleus of an atom
- Pauli exclusion principle
- a principle that states that no two electrons can have the same set of quantum numbers; that is, no two electrons can be in the same state
- shell
- a probability cloud for electrons that has a single principal quantum number
- subshell
- the probability cloud for electrons that has a single angular momentum quantum number


