01. Concepts and Principles
- Page ID
- 565
Concepts and Principles
To study the dynamics of an arbitrary rigid body we will break the motion down into a pure translation of the CM and a pure rotation about the CM. We will use particle dynamics, i.e., Newton's second law applied to the CM of the object, to study the translational portion of the motion. The study of the rotational portion of the motion requires a pair of new concepts. We will "invent" these concepts through the use of an analogy with linear dynamics.
In linear dynamics, Newton's second law states that the linear acceleration of an object is proportional to the total force acting on the object and inversely proportional to the mass, or inertia, of the object. It would seem plausible that the angular acceleratin of an object would depend on analogous concepts in the same manner.
We will replace the concept of force, often thought of as the push or pull applied to an object, with a quantity measuring the twist applied to an object. We will call this new quantity torque, symbolized t.
We will replace the concept of mass, the measure of the resistance of the object to changes in its linear velocity, with a quantity measuring the resistance of the object to changes in its angular velocity. We will call this new quantity rotational inertia, symbolized I.
In summary,
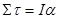
Before we go any further, however, let's define these new concepts more clearly.
Torque
In simple English, torque measures the twist applied to an object. The question remains, however, how do we quantify twist?
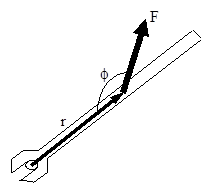
Let's examine a common device used to generate twist, a wrench. The magnitude, location, and orientation of the force applied to the wrench by the person's hand are indicated. Each of these three parameters effects the amount of twist the person delivers to the wrench (and therefore to the bolt).
If you've turned many bolts in your life, two things about this person's bolt-turning technique should grab you. First, why is this person applying the force at such a silly angle? She would generate much more twist if she applied the same magnitude force perpendicular to the wrench, rather than at an angle far from 900. Second, why is she not applying the force at the far edge of the wrench? She would generate far more twist if she applied the same magnitude force at the far edge of the wrench.
If the preceding paragraph makes sense to you, you understand how to quantify torque. To maximize torque, you should:
- Apply the force far from the axis of rotation (the bolt).
- Apply the force perpendicular to the position vector between the axis of rotation and the force.
- Apply a large magnitude force.
Mathematically, this is summarized by:
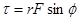
Note that this function has a maximum when r is large, F is large and = 900. Torque will also be assigned a direction, either clockwise or counterclockwise, depending upon the direction of the twist applied to the object. Use the Right Hand Rule to help determine the direction of the torque.

Rotational Inertia
We have constructed a rotatinal analogy to Newton's second law,
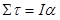
Our next task is to better define what we mean by I, the rotational inertia.
The rotational inertia is a measure of the resistance of the object to changes in its angular velocity. Imagine applying the same torque to two objects, initially at rest. After applying the torques for some set amount of time, measure the angular velocity of the objects. The object with the smaller angular velocity has the larger rotational inertia, because it has the larger resistance to angular acceleration.
Since more massive objects are harder to get moving linearly, it seems plausible that rotational inertia should depend on the mass of the object. It also seems plausible that rotational inertia should depend on the shape of the object.
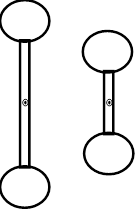
For example, it would be easier to get the smaller dumbbell spinning than the larger dumbbell, even though they have the same total mass.
Let's try to get more quantitative. Examining
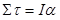
we can see that the units of I must be the units of torque (N.m) divided by the units of angular acceleration (s2). Remembering that a Newton is equivalent to kg.m.s2 leads to the units of rotational inertia being kg.m2. Thus, rotational inertia must be the product of a mass and a distance squared.
It seems plausible (there's that word again!) that the distance that is squared in the relationship for rotational inertia is the distance from the rotation axis. The farther a piece of mass is from the rotation axis, the more difficult it is to give the object an angular acceleration.

Enough with the "plausibilities", let's finally just define the rotational inertia to be:
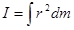
Imagine the object of interest divided into a large number of infinitesimally small chunks of mass, each with mass dm. Each chunk of mass is a distance r from the rotation axis. If you take the product of the mass of each chunk and the distance of the chunk from the rotation axis, squared, and sum this quantity over all the chunks of mass, you have the rotational inertia of the object of interest.
In summary, we now have quantitative relationships for measuring torque and rotational inertia,
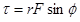
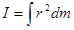
and the hypothesis that these two quantities are related in a manner analogous to Newton's second law,