5.1: Relative Position
- Page ID
- 33378
Relative to your eyes, your computer screen is about 3 feet away. Relative to the earth, the moon is 405,700 km far. In both these cases, we were able to define an arbitrary point of reference, i.e. your eyes and the earth. This is the principle of the relative position. In a region, we can choose an arbitrary reference point, and measure everything against/with reference to it.
Lets continue exploring this in 1D first and then generalize for n-dimensions.
1D Relative Position
Consider this line segment, with your friend at point A, you at point B and an ice-cream cart at point C. You and your friend are both lazy, but want to have ice-cream. You decide that who ever is closest to the cart will walk to the ice-cream cart and buy some for the both of you. Due to copyright, we assume you both are anthropomorphic balls.
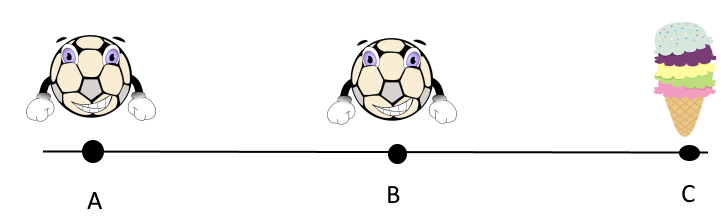
From the image, it is obvious that you are closer to the ice-cream cart. How can we prove this mathematically?
\(AC = AB + BC \)
\(\therefore BC = AC - AB \)
\(\therefore BC < AC \)
Hence, it is you who should fetch the ice-cream.
Let us now consider this scenario in 2D.
2D Relative Position
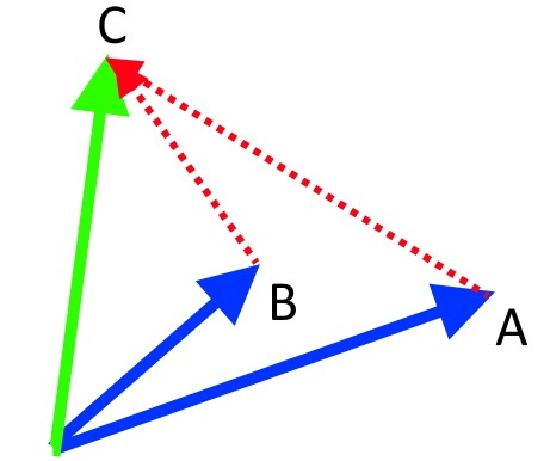
As above, your friend is at point A, you at B and the ice-cream cart at C. Initially, it might seem like a hard problem to solve, requiring the help of geometry. However, there is a much simpler way. We use vectors. Let \(\overrightarrow{A}, \overrightarrow{B}, \overrightarrow{C} \) represent the corresponding position vectors.
To find the distances AC and BC, we can use the magnitudes of vectors \(\overrightarrow{AC} \) and \(\overrightarrow{BC} \).
From the vectors chapter, we know that
\(\overrightarrow{AC} = \overrightarrow{C} - \overrightarrow{A} \)
\(\overrightarrow{BC} = \overrightarrow{C} - \overrightarrow{B} \)
We subtract the other vector from \(\overrightarrow{C} \) because C is our destination or final position. If we want just the magnitude, the sequence doesn't matter. But following the above sequence allows us to find the direction as well. (For more details about why this specific sequence, see shifting of origin)
What effectively happened was that we changed our point of reference from the origin to either A or B. At A, the distance from A should be zero. Hence, we subtract the position vector of our new origin (here, A or B) from the destination's position vector (here, C).
Conclusion
Using the above examples, we can generalize the relative position in this formula.
\(\overrightarrow{p}_{relative} = \overrightarrow{p}_{final} - \overrightarrow{p}_{initial} \)
Where \( \overrightarrow{p} \) is any position vector.

