2.2F: Potential in the Plane of a Charged Ring
- Page ID
- 5840
We suppose that we have a ring of radius a bearing a charge \(Q\). We shall try to find the potential at a point in the plane of the ring and at a distance \(r\) \((0 ≤ r < a)\) from the centre of the ring.
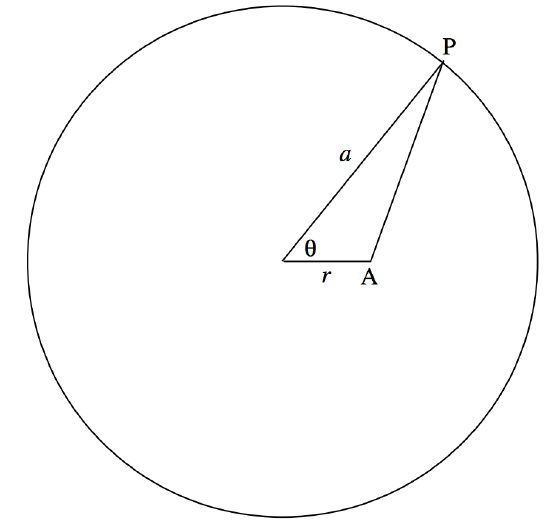
Consider an element \(δθ\) of the ring at P. The charge on it is \(\frac{Q\delta \theta}{2\pi}\). The potential at A due this element of charge is
\[\frac{1}{4\pi\epsilon_0}\cdot \frac{Q\delta \theta}{2\pi}\cdot \frac{1}{\sqrt{a^2+r^2-2ar\cos \theta}}=\frac{Q}{4\pi\epsilon_0 2\pi a}\cdot \frac{\delta \theta}{\sqrt{b-\cos \theta}},\tag{2.2.9}\]
where \(b=1+r^2/a^2\) and \(c = 2r / a\). The potential due to the charge on the entire ring is
\[V=\frac{Q}{4\pi\epsilon_0 \pi a}\int_0^\pi \frac{d\theta}{\sqrt{b-c\cos \theta}}.\tag{2.2.10}\]
I can’t immediately see an analytical solution to this integral, so I integrated it numerically from \(r = 0\) to \(r = 0.99\) in steps of \(0.01\), with the result shown in the following graph, in which \(r\) is in units of \(a\), and \(V\) is in units of \(\frac{Q}{4\pi\epsilon_0 a}\).
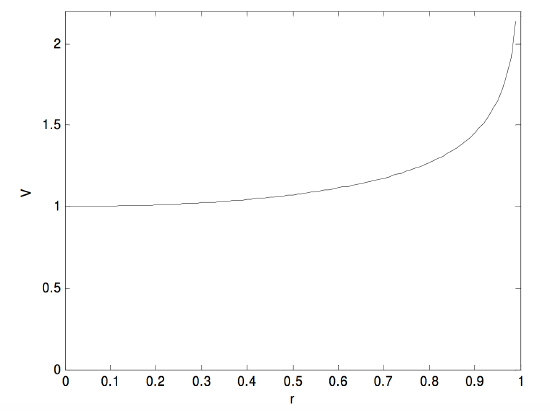
The field is equal to the gradient of this and is directed towards the centre of the ring. It looks as though a small positive charge would be in stable equilibrium at the centre of the ring, and this would be so if the charge were constrained to remain in the plane of the ring. But, without such a constraint, the charge would be pushed away from the ring if it strayed at all above or below the plane of the ring.
Some computational notes.
Any reader who has tried to reproduce these results will have discovered that rather a lot of heavy computation is required. Since there is no simple analytical expression for the integration, each of the 100 points from which the graph was computed entailed a numerical integration of the expression for the potential. I found that Simpson’s Rule did not give very satisfactory results, mainly because of the steep rise in the function at large \(r\), so I used Gaussian quadrature, which proved much more satisfactory.
Can we avoid the numerical integration? One possibility is to express the integrand in equation 2.2.10 as a power series in \(\cos θ\), and then integrate term by term.
Thus \(\sqrt{b-c\cos \theta}=\sqrt{b}\sqrt{1-e\cos \theta}\), where \(e=\frac{c}{b}=\frac{2(r/a)}{(r/a)^2+1}\). And then
\(\sqrt{1-r\cos \theta}=1+\frac{1}{2}e\cos \theta + \frac{3}{8}e^2 \cos^2 \theta +\frac{5}{16}e^3\cos^3 \theta +\frac{35}{128}e^4\cos^4 \theta + \frac{231}{1024}e^5 \cos^5 \theta +\frac{63}{256}e^6 \cos^6 \theta+\frac{231}{1024}e^7 \cos^7 \theta + \frac{715}{32768}e^8\cos^8 \theta + ... \tag{2.2.11}\)
We can then integrate this term by term, using \(\int_0^\pi \cos^n \theta \, d\theta = \frac{(n-1)!!\pi}{n!!}\) if \(n\) is even, and obviously zero if \(n\) is odd.
We finally get:
\[V=\frac{Q}{4\pi\epsilon_0 a}(1+\frac{3}{16}e^2+\frac{105}{1024}e^4+\frac{1155}{16384}e^6+\frac{25025}{4194304}e^8 ...).\tag{2.2.12}\]
For computational purposes, this is most efficiently rendered as
\[V=\frac{Q}{4\pi\epsilon_0 a}(1+e^2(\frac{3}{16}+e^4(\frac{105}{1024}+e^6(\frac{1155}{16384}+\frac{25025}{4194304}e^8)))).\tag{2.2.14}\]
I shall refer to this as Series I. It turns out that it is not a very efficient series, as it converges very slowly. This is because e is not a small fraction, and is always greater than \(r/a\). Thus for \(r/a=\frac{1}{2},\, e=0.8\).
We can do much better if we can obtain a power series in \(r/a\). Consider the expression \(\frac{1}{\sqrt{a^2+r^2-2ar\cos \theta}}=\frac{1}{a\sqrt{1+(r/a)^2-2(r/a)\cos \theta}}\), which occurs in equation 2.2.9. This expression, and others very similar to it, occur quite frequently in various physical situations. It can be expanded by the binomial theorem to give a power series in \(r/a\). (Admittedly, it is a trinomial expression, but do it in stages). The result is
\[(1+(r/a)^2-2(r/a)\cos \theta )^{-1/2}=P_0 (\cos \theta)+P_1(\cos \theta )(\frac{r}{a} ) + P_2 (\cos \theta)(\frac{r}{a})^2+P_3 (\cos \theta )(\frac{r}{a})^3 + ... \tag{2.2.15}\]
where the coefficients of the powers of \((\frac{r}{a})\) are polynomials in \(\cos θ\), which have been extensively tabulated in many places, and are called Legendre polynomials. See, for example my notes on Celestial Mechanics, http://orca.phys.uvic.ca/~tatum/celmechs.html Sections 1.1.4 and 5.11. Each term in the Legendre polynomials can then be integrated term by term, and the resulting series, after a bit of work, is
\[V=\frac{Q}{4\pi\epsilon_0 a}(1+\frac{1}{4}(\frac{r}{a})^2+\frac{9}{64}(\frac{r}{a})^4+\frac{25}{256}(\frac{r}{a})^6+\frac{1225}{16384}(\frac{r}{a})^8...).\tag{2.2.16}\]
Since this is a series in \((\frac{r}{a})\) rather than in \(e\), it converges much faster than equation 2.2.13. I shall refer to it as series \(II\). Of course, for computational purposes it should be written with nested parentheses, as we did for series I in equation 2.2.14.
Here is a table of the results using four methods. The first column gives the value of \(r/a\). The next four columns give the values of \(V\), in units of a \(\frac{Q}{4\pi\epsilon_0 a}\), calculated by four methods. Column 2, integration by Gaussian quadrature. Column 3, integration by Simpson’s Rule. Column 4, approximation by Series I. Column 5, approximation by series \(II\). In each case I have given the number of digits that I believe to be reliable. It is seen that Gaussian quadrature gives by far the best results. Series \(I\) is not very good at all, while Series \(II\) is almost as good as Simpson’s Rule.
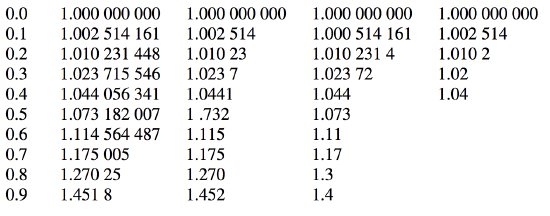
Of course any of these methods is completed almost instantaneously on a modern computer, so one may wonder if it is worthwhile spending much time seeking the most efficient solution. That will depend on whether one wants to do the calculation just once, or whether one wants to do similar calculations millions of times.


