3.3: Oscillation of a Dipole in an Electric Field
- Page ID
- 5426
Consider a dipole oscillating in an electric field (Figure III.3). When it is at an angle \(\theta\) to the field, the magnitude of the restoring torque on it is \(pE \sin \theta\), and therefore its equation of motion is
\[I\ddot \theta = -pE\sin \theta \label{1}\]
where \(I\) is its rotational inertia.
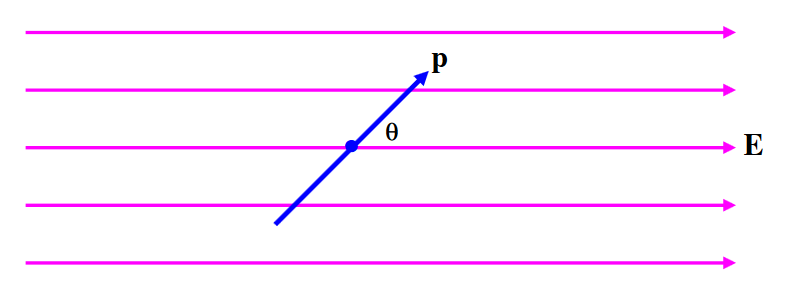
\(\text{FIGURE III.3}\)
For small angles, Equation \(\ref{1}\) can be approximated as
\[I\ddot \theta \approx -pE\theta\]
and so the period of small oscillations is
\[\label{3.3.1}P=2\pi\sqrt{\frac{I}{pE}}.\]
Would you expect the period to be long if the rotational inertia were large? Would you expect the vibrations to be rapid if \(p \text{ and }E\) were large? Is the above expression dimensionally correct?


