3.5: Force on a Dipole in an Inhomogeneous Electric Field
- Page ID
- 5428
 \(\text{FIGURE III.4}\)
\(\text{FIGURE III.4}\)
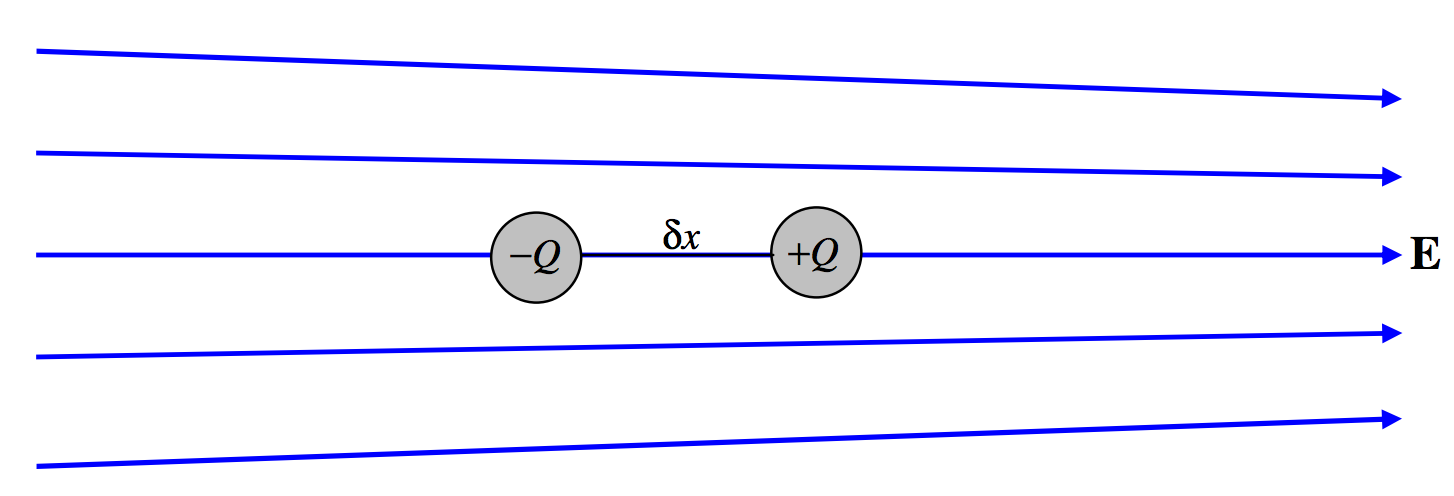
Consider a simple dipole consisting of two charges \(+Q\) and \(-Q\) separated by a distance \(δx\), so that its dipole moment is \(p = Q\, δx\). Imagine that it is situated in an inhomogeneous electrical field as shown in Figure \(III\).4. We have already noted that a dipole in a homogeneous field experiences no net force, but we can see that it does experience a net force in an inhomogeneous field. Let the field at \(−Q \text{ be }E\) and the field at \(+Q \text{ be }E + δE\). The force on \(−Q \text{ is }QE\) to the left, and the force on \(+Q \text{ is }Q(E + δE)\) to the right. Thus there is a net force to the right of \(Q\, δE\), or:
\[\label{3.5.1}\text{Force}=p\frac{dE}{dx}\]
Equation \ref{3.5.1} describes the situation where the dipole, the electric field and the gradient are all parallel to the x-axis. In a more general situation, all three of these are in different directions. Recall that electric field is minus potential gradient. Potential is a scalar function, whereas electric field is a vector function with three component, of which the x-component, for example is \(E_x=-\frac{∂V}{∂x}\). Field gradient is a symmetric tensor having nine components (of which, however, only six are distinct), such as \(\frac{∂^2V}{ ∂x^2},\,\frac{ ∂^2V}{ ∂y ∂z}\) etc. Thus in general Equation \ref{3.5.1} would have to be written as
\[\begin{pmatrix}E_x \\ E_y \\ E_z \\ \end{pmatrix} =-\begin{pmatrix}V_{xx} & V_{xy} & V_{xz} \\ V_{xy} & V_{yy} & V_{yz} \\ V_{xz} & V_{yz} & V_{zz} \\ \end{pmatrix}\begin{pmatrix}p_x \\ p_y \\ p_z \\ \end{pmatrix}\label{3.5.2}\]
in which the double subscripts in the potential gradient tensor denote the second partial derivatives.


