3.8: Quadrupole Moment
- Page ID
- 5765
Consider the system of charges shown in Figure \(III\).13. It has no net charge and no net dipole moment. Unlike a dipole, it will experience neither a net force nor a net torque in any uniform field. It may or may not experience a net force in an external nonuniform field. For example, if we think of the quadrupole as two dipoles, each dipole will experience a force proportional to the local field gradient in which it finds itself. If the field gradients at the location of each dipole are equal, the forces on each dipole will be equal but opposite, and there will be no net force on the quadrupole. If, however, the field gradients at the positions of the two dipoles are unequal, the forces on the two dipoles will be unequal, and there will be a net force on the quadrupole. Thus there will be a net force if there is a non-zero gradient of the field gradient. Stated another way, there will be no net force on the quadrupole if the mixed second partial derivatives of the field components (the third derivatives of the potential!) are zero. Further, if the quadrupole is in a nonuniform field, increasing, say, to the right, the upper pair will experience a force to the right and the lower pair will experience a force to the left; thus the system will experience a net torque in an inhomogeneous field, though there will be no net force unless the field gradients on the two pairs are unequal.
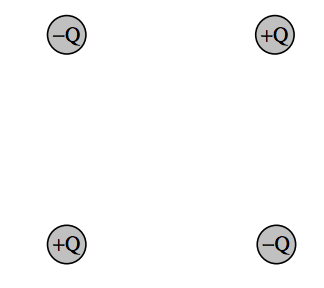
\(\text{FIGURE III.13}\)
The system possesses what is known as a quadrupole moment. While a single charge is a scalar quantity, and a dipole moment is a vector quantity, the quadrupole moment is a second order symmetric tensor.
The dipole moment of a system of charges is a vector with three components given by
\[\begin{align*} p_x &=\sum Q_i x_i \\[4pt] p_y &=\sum Q_iy_i \\[4pt] p_z &=\sum Q_i z_i . \end{align*}\]
The quadrupole moment \(\textbf{q}\) has nine components (of which six are distinct) defined by
\[q_{xx}=\sum Q_ix_i^2 \nonumber\]
\[ q_{xy}=\sum Q_ix_iy_i \nonumber\]
etc., and its matrix representation is
\[\textbf{q}=\begin{pmatrix} q_{xx} & q_{xy} & q_{xz} \\ q_{xy} & q_{yy} & q_{yz} \\ q_{xz} & q_{yz} & q_{zz} \\ \end{pmatrix}\label{3.8.1}\]
For a continuous charge distribution with charge density \(ρ\) coulombs per square metre, the components will be given by \(q_{xx}=\int \rho x^2 d\tau \), etc., where \(d\tau\) is a volume element, given in rectangular coordinates by \(dx\,dy\,dz\) and in spherical coordinates by \(r^2\sin θ\,dr\,dθ\,dφ\). The SI unit of quadrupole moment is C m2, and the dimensions are L2Q, By suitable rotation of axes, in the usual way (see for example section 2.17 of Classical Mechanics), the matrix can be diagonalized, and the diagonal elements are then the eigenvalues of the quadrupole moment, and the trace of the matrix is unaltered by the rotation.


