4.8: Power Delivered to an External Resistance
- Page ID
- 5972
Question: How much heat will be generated in the external resistance \(R \text{ if }R = 0\)?
Answer: None!
Question: How much heat will be generated in the external resistance \(R \text{ if }R = \infty\)?
Answer: None!
Question: How much heat will be generated in the external resistance \(R \text{ if }R \) is something?
Answer: Something!
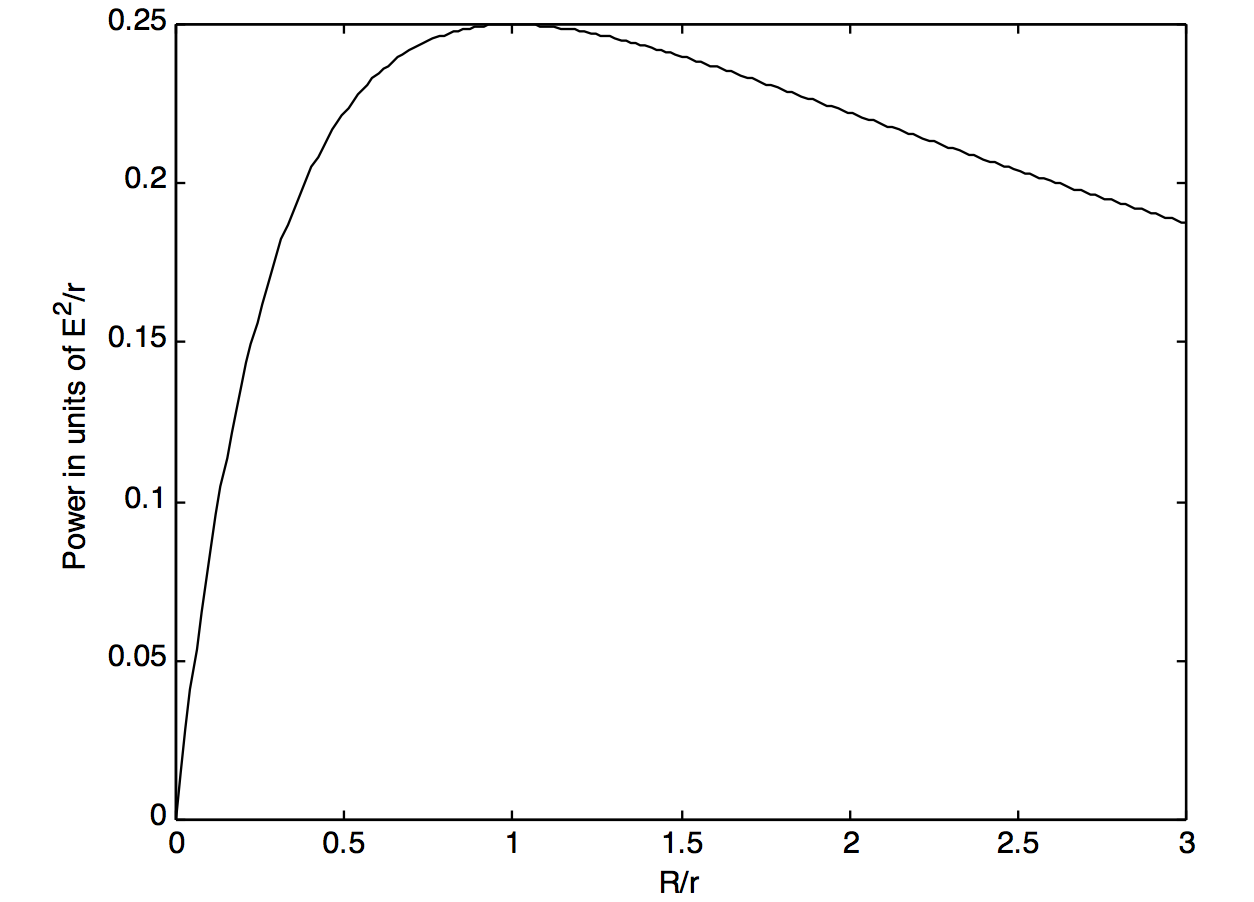
This suggests that there will be some value of the external resistance for which the power delivered, and heat generated, will be a maximum, and this is indeed the case.
The rate at which power is delivered, and dissipated as heat, is
\[P=I^2R=\frac{E^2R}{(R+r)^2}\label{4.8.1}\]
In Figure IV.5 I have plotted the power (in units of E 2/\(R\)) versus \(R/r\). Differentiation of the above expression (do it!) will show that the power delivered reaches a maximum of \(E^2/(4R)\) when \(R = r\); that is, when the external resistance is “matched” to the internal resistance of the cell. This is but one example of many in physics and engineering in which maximum power is delivered to a load when the load is matched to the internal load of the power source.
\(\text{FIGURE IV.5}\)


