4.12: Delta-Star Transform
- Page ID
- 5978
Consider the two circuits (each enclosed in a black box) of Figure IV.10.
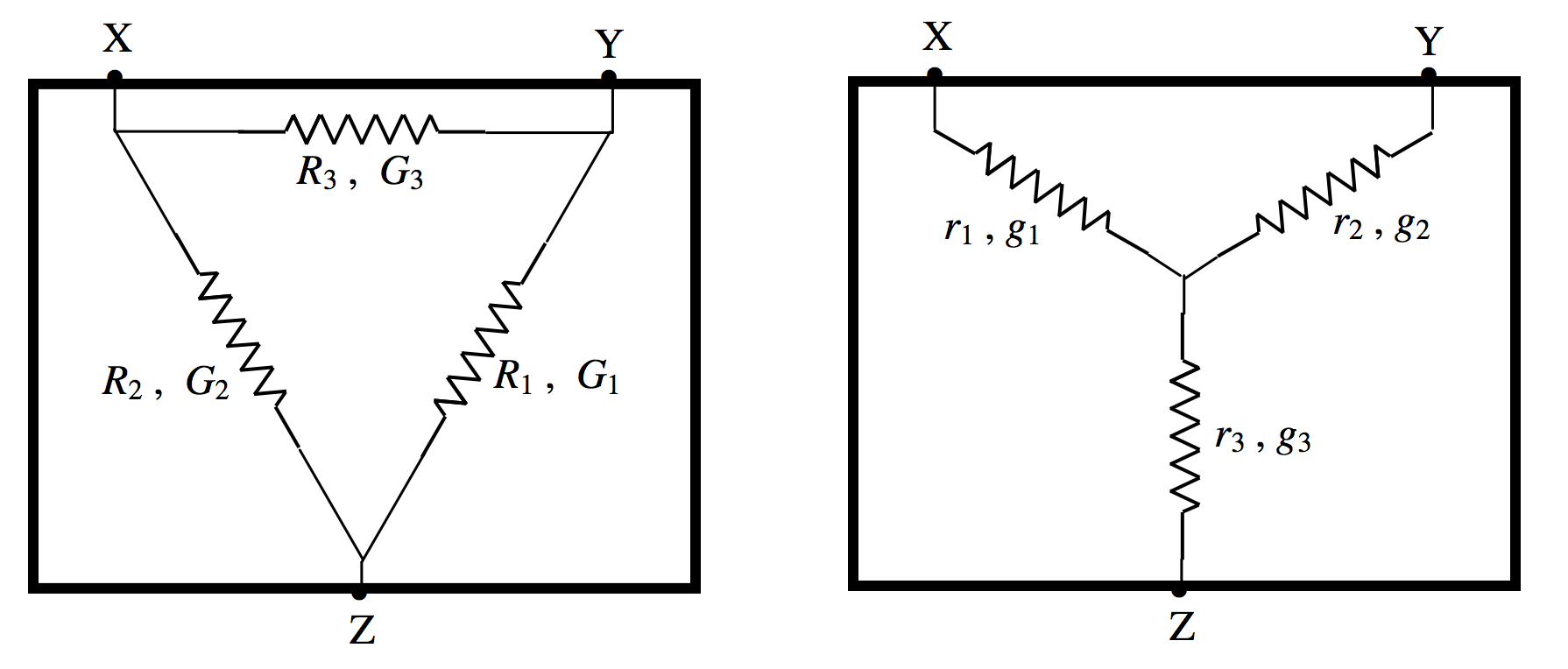
\(\text{FIGURE IV.10}\)
The configuration in the left hand box is called a “delta” (\(\Delta\)) and the configuration in the right hand box is called a “star” or a “Y”. I have marked against each resistor its resistance and its conductance, the conductance, of course, merely being the reciprocal of the resistance. I am going to suppose that the resistance between the terminals X and Y is the same for each box. In that case:
\[\label{4.12.1}r_1+r_2=\frac{R_3(R_1+R_2)}{R_1+R_2+R_3}.\]
We can get similar equations for the terminal pairs Y,Z and Z,X. Solving the three equations for r1, r2 and r3, we obtain
\[\begin{align}r_1&=\frac{R_2R_3}{R_1+R_2+R_3},\label{4.12.2} \\ r_2&=\frac{R_3R_1}{R_1+R_2+R_3},\label{4.12.3} \\ r_3&=\frac{R_1R_2}{R_1+R_2+R_3},\label{4.12.4} \\ \end{align}\]
In terms of the conductances, these are
\[\begin{align}g_1&=\frac{G_2G_3+G_3G_1+G_1G_2}{G_1},\label{4.12.5} \\ g_2&=\frac{G_2G_3+G_3G_1+G_1G_2}{G_2},\label{4.12.6} \\ g_3&=\frac{G_2G_3+G_3G_1+G_1G_2}{G_3},\label{4.12.7} \\ \end{align}\]
The converses of these equations are:
\[\begin{align}R_1&=\frac{r_2r_3+r_3r_1+r_1r_2}{r_1},\label{4.12.8} \\ R_2&=\frac{r_2r_3+r_3r_1+r_1r_2}{r_2},\label{4.12.9} \\ R_3&=\frac{r_2r_3+r_3r_1+r_1r_2}{r_3},\label{4.12.10} \\ G_1 &= \frac{g_2g_3}{g_1+g_2+g_3},\label{4.12.11} \\ G_2 &= \frac{g_3g_1}{g_1+g_2+g_3},\label{4.12.12} \\ G_3 &= \frac{g_1g_2}{g_1+g_2+g_3},\label{4.12.13} \\ \end{align}\]
That means that, if the resistances and conductances in one box are related to the resistances and conductances in the other by these equations, then you would not be able to tell, if you had an ammeter, and a voltmeter and an ohmmeter, which circuit was in which box. The two boxes are indistinguishable from their electrical behaviour.
These equations are not easy to commit to memory unless you are using them every day, and they are sufficiently awkward that mistakes are likely when evaluating them numerically. Therefore, to make the formulas useful, you should programme your calculator or computer so that they will instantly convert between delta and star without your ever having to think about it. The next example shows the formulas in use. It will be heavy work unless you have programmed your computer in advance – but if you have done so, you will see how very useful the transformations are.
Example. Calculate the resistance between the points A and B in the Figure below. The individual resistances are given in ohms.
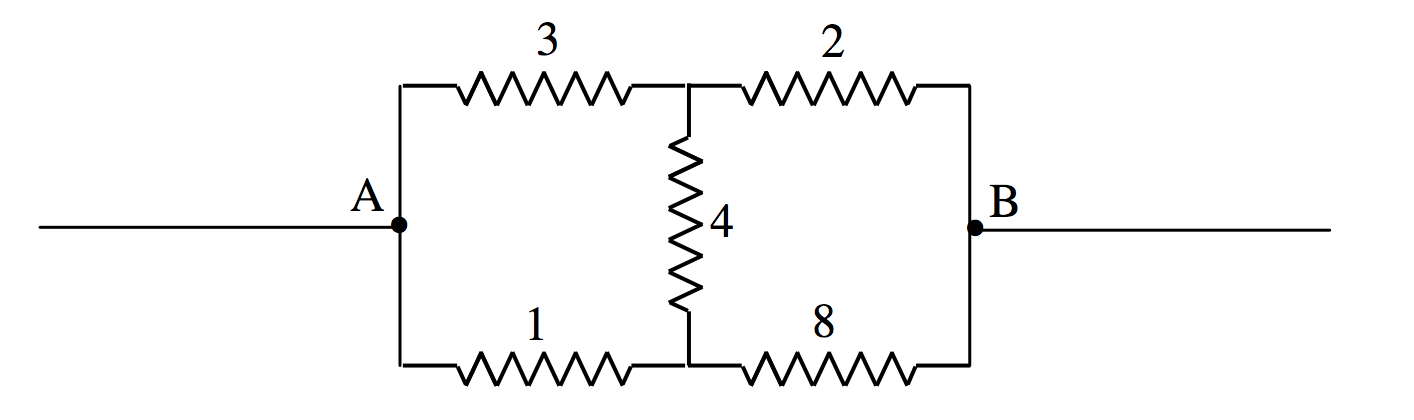
At first, one doesn’t know how to start. But notice that the 1, 3 and 4 ohm resistors are connected in delta and the circuit is therefore equivalent to
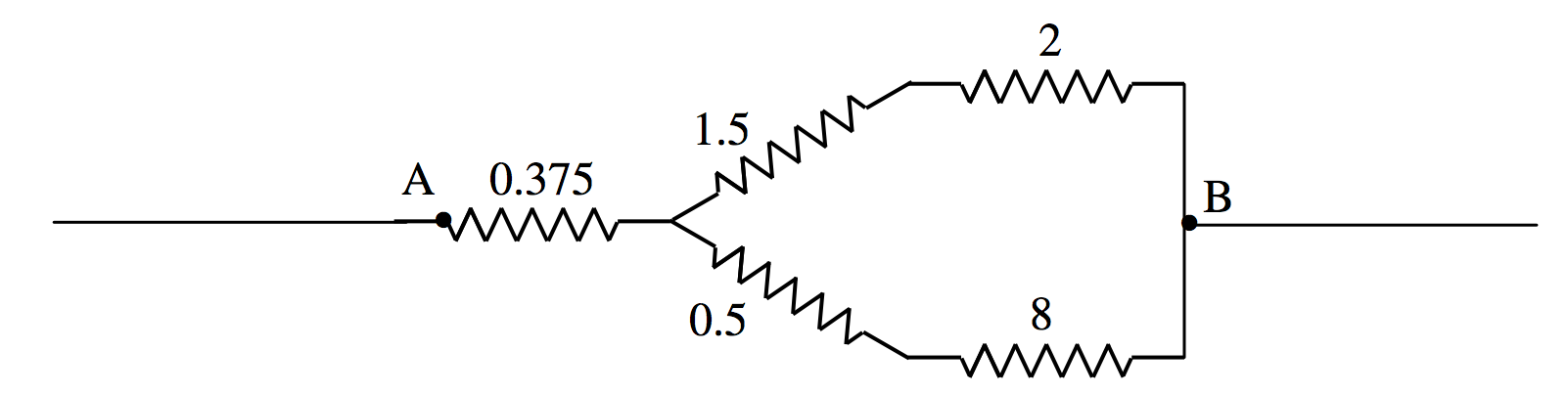
After that, it is easy, and you will soon find that the resistance between A and B is 2.85 \(\Omega\).


