9.5: Uniform Plane Waves - Characteristics
( \newcommand{\kernel}{\mathrm{null}\,}\)
In Section 9.4, expressions for the electric and magnetic fields are determined for a uniform plane wave in lossless media. If the planar phasefront is perpendicular to the z axis, then waves may propagate in either the +ˆz direction of the −ˆz direction. If we consider only the former, and select ˜E to point in the +ˆx direction, then we find
˜E=+ˆxE0e−jβz
˜H=+ˆyE0ηe−jβz
where β=ω√μϵ is the phase propagation constant, η=√μ/ϵ is the wave impedance, and E0 is a complex-valued constant associated with the magnitude and phase of the source. This result is in fact completely general for uniform plane waves, since any other possibility may be obtained by simply rotating coordinates. In fact, this is pretty easy because (as determined in Section 9.4) ˜E, ˜H, and the direction of propagation are mutually perpendicular, with the direction of propagation pointing in the same direction as ˜EטH.
In this section, we identify some important characteristics of uniform plane waves, including wavelength and phase velocity. Chances are that much of what appears here will be familiar to the reader; if not, a quick review of Sections 1.3 (“Fundamentals of Waves”) and 3.8 (“Wave Propagation on a Transmission Line”) are recommended.
First, recall that ˜E and ˜H are phasors representing physical (real-valued) fields and are not the field values themselves. The actual, physical electric field intensity is
E=Re{˜Eejωt}=Re{ˆxE0e−jβzejωt}=ˆx|E0|cos(ωt−βz+ψ)
where ψ is the phase of E0. Similarly: H=ˆy|E0|ηcos(ωt−βz+ψ) This result is illustrated in Figure 9.5.1. Note that both E and H (as well as their phasor representations) have the same phase and have the same frequency and position dependence cos(ωt−βz+ψ). Since β is a real-valued constant for lossless media, only the phase, and not the magnitude, varies with z. If ω→0, then β→0 and the fields no longer depend on z; in this case, the field is not propagating. For ω>0, cos(ωt−βz+ψ) is periodic in z; specifically, it has the same value each time z increases or decreases by 2π/β. This is, by definition, the wavelength λ: λ≜2πβ
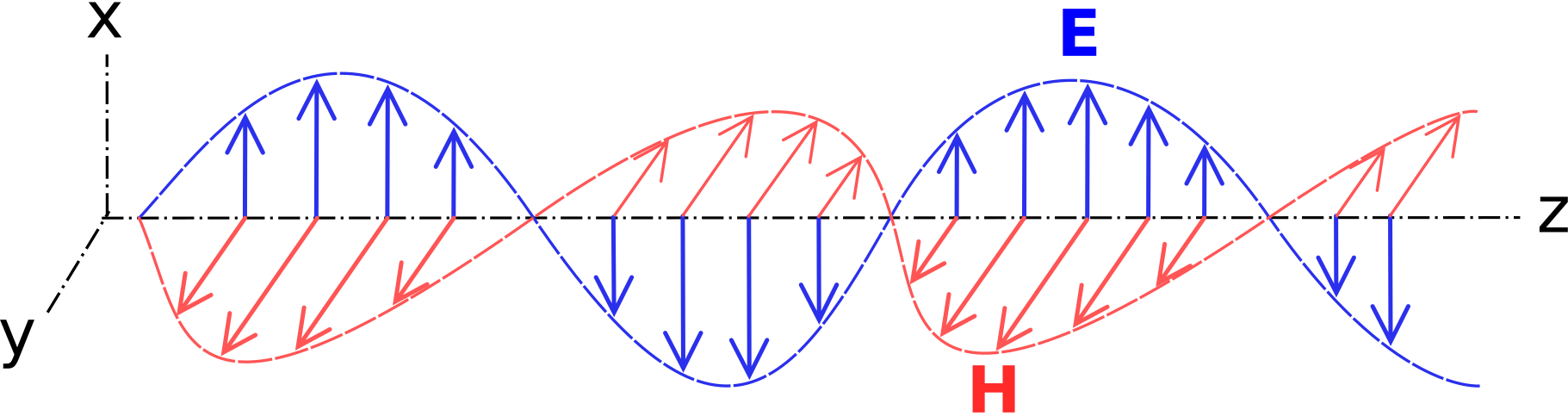 Figure 9.5.1: Relationship between the electric field direction, magnetic field direction, and direction of propogation (here, +ˆz(© (Modified) CC BY SA 3.0; E. Boutet)
Figure 9.5.1: Relationship between the electric field direction, magnetic field direction, and direction of propogation (here, +ˆz(© (Modified) CC BY SA 3.0; E. Boutet)
If we observe this wave at some fixed point (i.e., hold z constant), we find that the electric and magnetic fields are also periodic in time; specifically, they have the same value each time t increases by 2π/ω. We may characterize the speed at which the wave travels by comparing the distance required to experience 2π of phase rotation at a fixed time, which is 1/β; to the time it takes to experience 2π of phase rotation at a fixed location, which is 1/ω. This is known as the phase velocity1 vp:
vp≜1/β1/ω=ωβ
Note that vp has the units expected from its definition, namely (rad/s)/(rad/m) = m/s. If we make the substitution β=ω√μϵ, we find
vp=ωω√μϵ=1√μϵ
Note that vp, like the wave impedance η, depends only on material properties. For example, the phase velocity of an electromagnetic wave in free space, given the special symbol c, is
c≜vp|μ=μ0,ϵ=ϵ0=1√μ0ϵ0≅3.00×108 m/s
This constant is commonly referred to as the speed of light, but in fact it is the phase velocity of an electromagnetic field at any frequency (not just optical frequencies) in free space. Since the permittivity ϵ and permeability μ of any material is greater than that of a vacuum, vp in any material is less than the phase velocity in free space. Summarizing:
Phase velocity is the speed at which any point of constant phase appears to travel along the direction of propagation.
Phase velocity is maximum (=c) in free space, and slower by a factor of 1/√μrϵr in any other lossless medium.
Finally, we note the following relationship between frequency f, wavelength, and phase velocity: λ=2πβ=2πω/vp=2π2πf/vp=vpf Thus, given any two of the parameters f, λ, and vp, we may solve for the remaining quantity. Also note that as a consequence of the inverse-proportional relationship between λ and vp, we find:
At a given frequency, the wavelength in any material is shorter than the wavelength in free space.
Polyethylene is a low-loss dielectric having ϵr≅2.3. What is the phase velocity in polyethylene? What is wavelength in polyethylene? The frequency of interest is 1 GHz.
Solution
Low-loss dielectrics exhibit μr≅1 and σ≈0. Therefore the phase velocity is
vp=1√μ0ϵrϵ0=c√ϵr≅1.98×108 m/s
i.e., very nearly two-thirds of the speed of light in free space. The wavelength at 1 GHz is
λ=vpf≅19.8 cm
Again, about two-thirds of a wavelength at the same frequency in free space.
Returning to polarization and magnitude, it is useful to note that Equation ??? could be written in terms of E as follows: H=1ηˆz×E i.e., H is perpendicular to both the direction of propagation (here, +ˆz) and E, with magnitude that is different from E by the wave impedance η. This simple expression is very useful for quickly determining H given E when the direction of propagation is known. In fact, it is so useful that it commonly explicitly generalized as follows:
H=1ηˆk×E
where ˆk (here, +ˆz) is the direction of propagation. Similarly, given H, ˆk, and η, we may find E using
E=−ηˆk×H
These spatial relationships can be readily verified using Figure 9.5.1.
Equations ??? and ??? are known as the plane wave relationships.
The plane wave relationships apply equally well to the phasor representation of bfE and H; i.e.,
˜E=−ηˆkטH˜H=1ηˆkטE
These equations can be readily verified by applying the definition of the associated phasors (e.g., Equation 9.5.3). It also turns out that these relationships apply at each point in space, even if the waves are not planar, uniform, or in lossless media.
Consider the scenario illustrated in Figure 9.5.2.
 Figure 9.5.2: A radially-directed plane wave.
Figure 9.5.2: A radially-directed plane wave.
Here a uniform plane wave having frequency f=3 GHz is propagating along a path of constant ϕ, where is ϕ is known but not specified. The phase of the electric field is π/2 radians at ρ=0 (the origin) and t=0. The material is an effectively unbounded region of free space. The electric field is oriented in the +ˆz direction and has peak magnitude of 1 mV/m. Find (a) the electric field intensity in phasor representation, (b) the magnetic field intensity in phasor representation, and (c) the actual, physical electric field along the radial path.
Solution
First, realize that this “radially-directed” plane wave is in fact a plane wave, and not a cylindrical wave. It may well we be that if we “zoom out” far enough, we are able to perceive a cylindrical wave (for more on this idea, see Section 9.3), or it might simply be that wave is exactly planar, and cylindrical coordinates just happen to be a convenient coordinate system for this application. In either case, the direction of propagation ˆk=+ˆρ and the solution to this example will be the same.
Here’s the phasor representation for the electric field intensity of a uniform plane wave in a lossless medium, analogous to Equation ???:
˜E=+ˆzE0e−jβρ
From the problem statement, |E0|=1 mV/m. Also from the problem statement, the phase of E0 is π/2 radians; in fact, we could just write E0=+j|E0|. Thus, the answer to (a) is ˜E=+ˆzj|E0|e−jβρ where the propagation constant β=ω√μϵ=2πf√μ0ϵ0≅62.9 rad/m.
The answer to (b) is easiest to obtain from the plane wave relationship:
˜H=1ηˆk×E=1ηˆρ×(+ˆzj|E0|e−jβρ)=−ˆϕj|E0|ηe−jβρ
where η here is √μ0/ϵ0≅377 Ω. Thus, the answer to part (b) is ˜H=−ˆϕjH0e−jβρ where H0≅2.65 μA/m. At this point you should check vector directions: ˜EטH should point in the direction of propagation +ˆρ. Here we find ˆz×(−ˆϕ)=+ˆρ, as expected.
The answer to (c) is obtained by applying the defining relationship for phasors to the answer to part (a):
E=Re{˜Eejωt}=Re{(+ˆzj|E0|e−jβρ)ejωt}=+ˆz|E0|Re{ejπ/2e−jβρejωt}=+ˆz|E0|cos(ωt−βρ+π2)
- We acknowledge that this is a misnomer, since velocity is properly defined as speed in a specified direction, and vp by itself does not specify direction. In fact, the phase velocity in this case is properly said to be +ˆzvp. Nevertheless, we adopt the prevailing terminology.↩


