5.3: Coaxial Cylindrical Capacitor
( \newcommand{\kernel}{\mathrm{null}\,}\)
The radii of the inner and outer cylinders are a and b, and the permittivity between them is ϵ.
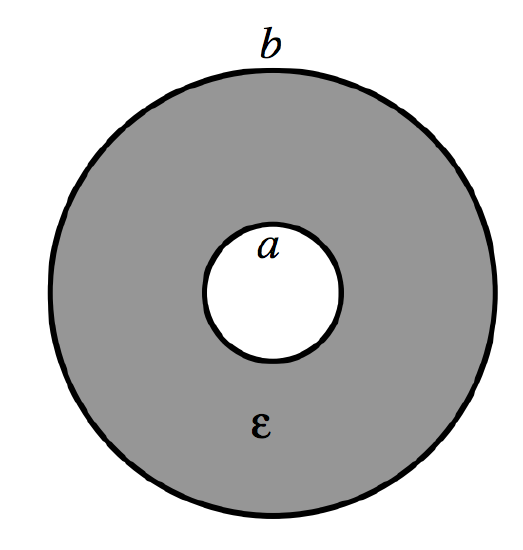
FIGURE V.4
Suppose that the two cylinders are connected to a battery so that the potential difference between them is V, and the charge per unit length on the inner cylinder is +λC m−1, and on the outer cylinder is −λC m−1. We have seen (Subsection 2.2.3) that the potential difference between the cylinders under such circumstances is λ2πϵln(b/a). Therefore the capacitance per unit length, C′, is
C′=2πϵln(b/a).
This is by no means solely of academic interest. The capacitance per unit length of coaxial cable (“coax”) is an important property of the cable, and this is the formula used to calculate it.


