2.6: The unimodular group SL(n, R) and the invariance of volume

It is well known that the volume of a parallelepiped spanned by linearly independent vectors is given by the determinant of the vector components. It is evident therefore that a transformation with a unimodular matrix leaves this expression for the volume invariant.

Yet the situation has some subtle aspects which call for a closer examination. Although the calculation of volume and area is among the standard procedures of geometry, this is usually carried out in metric spaces, in which length and angle have their well known Euclidean meaning. However, this is a too restrictive assumption, and the determinantal formula can be justified also within affine geometry without using metric concepts.

Since we shall repeatedly encounter such situations, we briefly explain the underlying idea for the case of areas in a two-dimensional vector space \(V(2, R)\).

We advance two postulates:

1. Area is an additive quantity: the area of a figure is equal to the sum of the areas of its parts.

2. Translationally congruent figures have equal areas.

(The point is that Euclidean congruence’involves also rotational congruence, which is not available to us because of the absence of metric.) We proceed now in successive steps as shown in Figure 2.2.

Figure 2.2: Translational congruence and equal area.

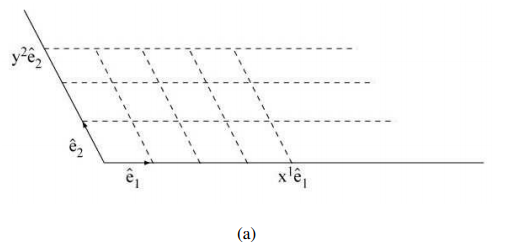
Consider at first the vectors

\[\begin{array}{l}
\vec{x}=x^{1} \vec{e}_{1} \\
\vec{y}=y^{2} \vec{e}_{2}
\end{array}\]

where the coordinates are integers (Figure 2.2a). The area relative to the unit cell is obtained through simple counting as \(x^{1} y^{2}\). The same result can be justified for any real values for the coordinates by subdivision and a limiting process.

We are permitted to write this result in determinantal form:

\[x^{1} y^{2}=\left|\begin{array}{cc}
x^{1} & 0 \\
0 & y^{2}
\end{array}\right|\label{1}\]

If the vectors

\[\begin{array}{l}
\vec{x}=x^{1} \vec{e}_{1}+x^{2} \vec{e}_{2} \\
\vec{y}=y^{1} \vec{e}_{1}+y^{2} \vec{e}_{2}
\end{array}\]

do not coincide with the coordinate axes, the coincidence can be achieved in no more than two steps (Figures 2.2b and 2.2c) using the translational congruence of the parallelograms (0123) (012’3’) (012”3’).

By an elementary geometrical argument one concludes from here that the area spanned by \(\vec{x} \text { and } \vec{y}\) is equal to the area spanned by \(\hat{e}_{1} \text { and } \hat{e}_{2}\) multiplied by the determinant

\[\left|\begin{array}{ll}
x^{1} & x^{2} \\
y^{1} & y^{2}
\end{array}\right|\label{2}\]

This result can be justified also in a more elegant way: The geometrical operations in figures b and c consist of adding the multiple of the vector \(\vec{y} \text { to the vector } \vec{x}\), or adding the multiple of the second row of the determinant to the first row, and we know that such operations leave the value of the determinant unchanged.

The connection between determinant and area can be generalized to three and more dimensions, although the direct geometric argument would become increasingly cumbersome.

This defect will be remedied most effectively in terms of the Grassmann algebra that will be developed in Chapter VII.