7.1: Complex Continuity and Differentiability

The concept of a continuous complex function makes use of an “epsilon-delta definition”, similar to the definition for functions of real variables (see Chapter 1):

Definition: Word

A complex function \(f(z)\) is continuous at \(z_0 \in \mathbb{C}\) if, for any \(\epsilon > 0\), we can find a \(\delta > 0\) such that \[\big|\, z - z_0 \,\big| < \delta \;\;\; \Rightarrow \;\;\; \big|\, f(z) - f(z_0) \,\big| < \epsilon.\]

Here, \(\big|\cdots\big|\) denotes the magnitude of a complex number. If you have difficulty processing this definition, don’t worry; it basically says that as \(z\) is varied smoothly, there are no abrupt jumps in the value of \(f(z)\).

If a function is continuous at a point \(z\), we can define its complex derivative as \[f'(z) = \frac{df}{dz} = \lim_{\delta z\rightarrow 0} \frac{f(z+\delta z) - f(z)}{\delta z}.\] This is very similar to the definition of the derivative for a function of a real variable (see Chapter 1). However, there’s a complication which doesn’t appear in the real case: the infinitesimal \(\delta z\) is a complex number, not just a real number, yet the above definition does not specify the argument of \(\delta z\). The choice of the argument of \(\delta z\) is equivalent to the direction in the complex plane in which \(\delta z\) points, as shown in the following figure:

Figure \(\PageIndex{1}\)

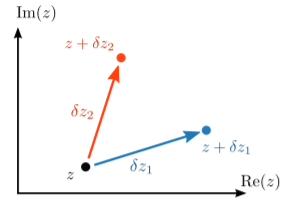
In principle, we might get different results from the above formula when we plug in different infinitesimals \(\delta z\), even in the limit where \(\delta z \rightarrow 0\) and even though \(f(z)\) is continuous.

Example \(\PageIndex{1}\)

Consider the function \(f(z) = z^*\). According to the formula for the complex derivative, \[\lim_{\delta z \rightarrow0} \frac{f(z+\delta z) - f(z)}{\delta z} = \lim_{\delta z \rightarrow0} \frac{z^*+\delta z^* - z^*}{\delta z} = \lim_{\delta z \rightarrow0} \frac{\delta z^*}{\delta z}.\] But if we plug in a real \(\delta z\), we get a different result than if we plug in an imaginary \(\delta z\): \[\begin{align} \delta z \in \mathbb{R} \;\; &\Rightarrow \frac{\delta z^*}{\delta z} = 1.\\ \delta z \in i \cdot \mathbb{R} &\Rightarrow \frac{\delta z^*}{\delta z} = -1.\end{align}\]

We can deal with this complication by regarding the complex derivative as well-defined only if the above definition gives the same answer regardless of the argument of \(\delta z\). If a function satisfies this property at a point \(z\), we say that the function is complex-differentiable at \(z\).

The preceding example showed that \(f(z) = z^*\) is not complex-differentiable for any \(z \in \mathbb{C}\). On the other hand, the following example shows that the function \(f(z) = z\) is complex-differentiable for all \(z \in \mathbb{C}\):

Example \(\PageIndex{2}\)

The function \(f(z) = z\) is complex differentiable for any \(z \in \mathbb{C}\), since \[\lim_{\delta z \rightarrow0} \frac{f(z+\delta z) - f(z)}{\delta z} = \lim_{\delta z \rightarrow0} \frac{z+\delta z - z}{\delta z} = \lim_{\delta z \rightarrow0} \frac{\delta z}{\delta z} = 1.\] The reason the result doesn’t depend on the argument of \(\delta z\) is that the derivative formula simplifies to the fraction \(\delta z / \delta z\), which is equal to 1 for any \(|\delta z| > 0\). Note that we simplify the fraction to 1 before taking the limit \(\delta z \rightarrow 0\). We can’t take the limit first, because \(0/0\) is undefined.