1.4: Real and Apparent Depth
- Page ID
- 7069
When we look down into a pool of water from above, the pool looks less deep than it really is. Figure I.6 shows the formation of a virtual image of a point on the bottom of the pool by refraction at the surface.
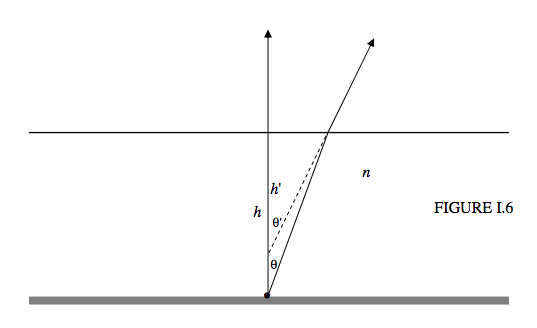
The diameter of the pupil of the human eye is in the range 4 to 7 mm, so, when we are looking down into a pool (or indeed looking at anything that is not very close to our eyes), the angles involved are small. Thus in Figure I.6 you are asked to imagine that all the angles are small; actually to draw them small would make for a very cramped drawing. Since angles are small, I can approximate Snell’s law:
\[\begin{align} n &= \frac{\sin \theta '}{\sin \theta} \label{eq2} \\[4pt] & \approx \dfrac{ \tan \theta ' }{ \tan \theta } \label{eq:1.4.1} \end{align} \]
and hence
\[ \frac{\text{real depth}}{\text{apparent depth}}=\frac{h}{h'}=\frac{\tan \theta'}{\tan \theta} = n. \label{eq:1.4.2} \]
For water, \(n\) is about \(\frac{4}{3}\), so that the apparent depth is about \(\frac{3}{4}\) of the real depth.
Exercise \(\PageIndex{1}\)
An astronomer places a photographic film, or a CCD, at the primary focus of a telescope. He then decides to insert a glass filter, of refractive index \(n\) and thickness \(t\), in front of the film (or CCD). In which direction should he move the film or CCD, and by how much, so that the image remains in focus?
Now if Snell’s law really were given by Equation \(\ref{eq:1.4.1}\), all refracted rays from the object would, when produced backwards, appear to diverge from a single point, namely the virtual image. But Snell’s law is really Equation \ref{eq2}, so what happens if we do not make the small angle approximation?
We have
\[ \dfrac{h}{h'} = \frac{\tan \theta'}{\tan \theta}\]
and, if we apply the trigonometric identity
\[\tan \theta = \frac{\sin \theta}{\sqrt{1- \sin^2 \theta}} \]
and apply Snell’s law (Equation \ref{eq2}), we find that
\[ \frac{h}{h'} = \frac{n \cos \theta}{\sqrt{1-n^2 \sin^2 \theta}} \label{eq:1.4.3} \]
Exercise \(\PageIndex{2}\)
Show that, to first order in \( \theta \) that Equation \ref{eq:1.4.3} becomes \(h/h' = n\).
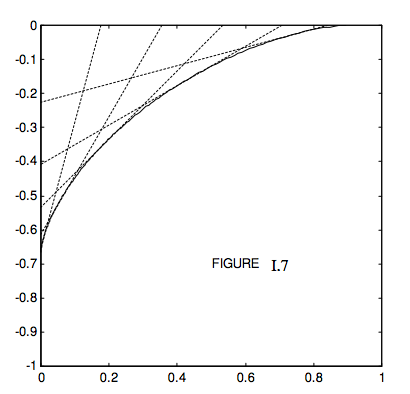
Equation \(\ref{eq:1.4.3}\) shows \(h'\) as a function of \( \theta \) − and that the refracted rays, when projected backwards, do not all appear to come from a single point. In other words, a point object does not result in a point image. Figure I.7 shows (for \(n = 1.5\) – i.e. glass rather than water) the backward projections of the refracted rays for \( \theta '\)= 15, 30, 45, 60 and 75 degrees, together with their envelope or “caustic curve”. The “object” is at the bottom left corner of the frame, and the surface is the upper side of the frame.
Exercise \(\PageIndex{3}\)
(for the mathematically comfortable). Show that the parametric equations for the caustic curve are
\[ x-y \tan \theta' - h \tan \theta = 0 \nonumber\]
and
\[ ny \sec^3 \theta ' + h \sec^3 \theta = 0. \nonumber \]
Here, \(y = 0\) is taken to be the refracting surface, and \( \theta\) and \( \theta ' \) are related by Snell’s law.
Thus refraction at a plane interface produces an aberration in the sense that light from a point object does not diverge from a point image. This type of aberration is somewhat similar to the type of aberration produced by reflection from a spherical mirror, and to that extent the aberration could be referred to as “spherical aberration”. If a point at the bottom of a pond is viewed at an angle to the surface, rather than perpendicular to it, a further aberration called “astigmatism” is produced. This will be discussed in Chapter 4.


