2.13: The Lazy Way
- Page ID
- 8306
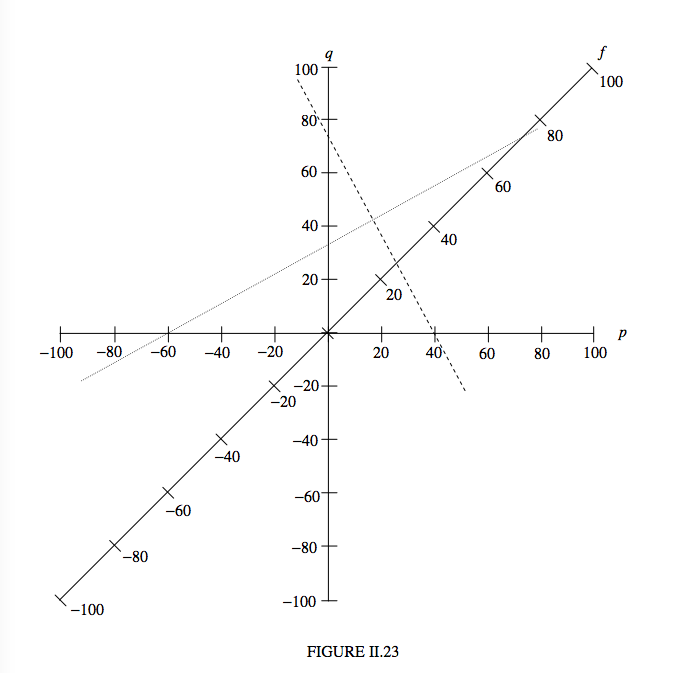
The convergence and power method has great advantages when you have a complex systems of many lenses, mirrors and interfaces in succession. You just add the powers one after the other. But I expect there are some readers who don’t want to be bothered with all of that, and just want to do simple single-lens calculations with a simple formula that they are accustomed to, in particular the well-known \( \frac{1}{p}+ \frac{1}{q}=\frac{1}{f},\), which is appropriate for the “real is positive” sign convention – and they want to get the calculation over with as soon as possible and with as little effort as possible. This section is for them! I have drawn a simple diagram in Figure II.23. It is not extremely accurate – it is the best I can do with this infernal machine that I am sitting in front of. All you need in order to draw a really good version of it is a sheet of graph paper. There are three axes, labelled \(p\), \(q\) and \(f\). For any particular problem, to solve the above equation, all you do is to lay the edge of a ruler across the figure. For example: \(p\) = 40 cm, \(f\) = 26 cm. What is \(q\)? The dashed line gives the answer: \(q = 75 \)cm. Another example: \(p = 33 \) cm, \(q = −60 \) cm. What is \(f\)? The dotted line gives the answer: \(f = 73\) cm.
This diagram can also be used for resistors in parallel, capacitors in series, synodic and sidereal periods of planets...