1.2: Operators in Hilbert Space

The objects \(|\psi\rangle\) are vectors in a Hilbert space. We can imagine applying rotations of the vectors, rescaling, permutations of vectors in a basis, and so on. These are described mathematically as operators, and we denote them by capital letters A, B, C, etc. In general we write

\[A|\phi\rangle=|\psi\rangle\tag{1.6}\]

for some \( |\phi\rangle, |\psi\rangle \in\) 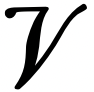. It is important to remember that operators act on all the vectors in Hilbert space. Let \(\left\{\left|\phi_{j}\right\rangle\right\}_{j}\) be an orthonormal basis. We can calculate the inner product between the vectors \(\left|\phi_{j}\right\rangle\) and A \(\left|\phi_{k}\right\rangle\):

\[\left\langle\phi_{j}\right|\left(A\left|\phi_{k}\right\rangle\right)=\left\langle\phi_{j}|A| \phi_{k}\right\rangle \equiv A_{j k}\tag{1.7}\]

The two indices indicate that operators are matrices.

As an example, consider two vectors, written as two-dimensional column vectors

\[\left|\phi_{1}\right\rangle=\left(\begin{array}{l}
1 \\
0
\end{array}\right), \quad\left|\phi_{2}\right\rangle=\left(\begin{array}{l}
0 \\
1
\end{array}\right)\tag{1.8}\]

and suppose that

\[A=\left(\begin{array}{ll}
2 & 0 \\
0 & 3
\end{array}\right)\tag{1.9}\]

We calculate

\[A_{11}=\left\langle\phi_{1}|A| \phi_{1}\right\rangle=(1,0) \cdot\left(\begin{array}{ll}
2 & 0 \\
0 & 3
\end{array}\right)\left(\begin{array}{l}
1 \\
0
\end{array}\right)=(1,0) \cdot\left(\begin{array}{l}
2 \\
0
\end{array}\right)=2\tag{1.10}\]

Similarly, we can calculate that \(A_{22}=3\), and \(A_{12}=A_{21}=0\) (check this). We therefore have that \(A\left|\phi_{1}\right\rangle=2\left|\phi_{1}\right\rangle\) and \(A\left|\phi_{2}\right\rangle=3\left|\phi_{2}\right\rangle\).

Complex numbers \(a\) have complex conjugates \(a^{*}\) and vectors \(|\psi\rangle\) have dual vectors \(\langle\phi|\). Is there an equivalent for operators? The answer is yes, and it is called the adjoint, or Hermitian conjugate, and is denoted by a dagger \(\dagger\). The natural way to define it is according to the rule

\[\langle\psi|A| \phi\rangle^{*}=\left\langle\phi\left|A^{\dagger}\right| \psi\right\rangle\tag{1.11}\]

for any \(|\phi\rangle\) and \(|\psi\rangle\). In matrix notation, and given an orthonormal basis \(\left\{\left|\phi_{j}\right\rangle\right\}_{j}\), this becomes

\[\left\langle\phi_{j}|A| \phi_{k}\right\rangle^{*}=A_{j k}^{*}=\left\langle\phi_{k}\left|A^{\dagger}\right| \phi_{j}\right\rangle=A_{k j}^{\dagger}\tag{1.12}\]

So the matrix representation of the adjoint \(A^{\dagger}\) is the transpose and the complex conjugate of the matrix A, as given by \(\left(A^{\dagger}\right)_{j k}=A_{k j}^{*}\). The adjoint has the following properties:

1. \((c A)^{\dagger}=c^{*} A^{\dagger}\),
2. \((A B)^{\dagger}=B^{\dagger} A^{\dagger}\),
3. \((|\phi\rangle)^{\dagger}=\langle\phi|\).

Note the order of the operators in 2: AB is generally not the same as BA. The difference between the two is called the commutator, denoted by

\[[A, B]=A B-B A\tag{1.13}\]

For example, we can choose

\[A=\left(\begin{array}{ll}
0 & 1 \\
1 & 0
\end{array}\right) \quad \text { and } \quad B=\left(\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right)\tag{1.14}\]

which leads to

\[\begin{aligned}{}
[A, B] &=\left(\begin{array}{ll}
0 & 1 \\
1 & 0
\end{array}\right)\left(\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right)-\left(\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right)\left(\begin{array}{cc}
0 & 1 \\
1 & 0
\end{array}\right)=\left(\begin{array}{cc}
0 & -1 \\
1 & 0
\end{array}\right)-\left(\begin{array}{cc}
0 & 1 \\
-1 & 0
\end{array}\right) \\
&=\left(\begin{array}{cc}
0 & -2 \\
2 & 0
\end{array}\right) \neq 0 .
\end{aligned}\tag{1.15}\]

Many, but not all, operators have an inverse. Let \(A|\phi\rangle=|\psi\rangle\) and \(B|\psi\rangle=|\phi\rangle\). Then we have

\[B A|\phi\rangle=|\phi\rangle \quad \text { and } \quad A B|\psi\rangle=|\psi\rangle\tag{1.16}\]

If Eq. (1.16) holds true for all \(|\phi\rangle\) and \(|\psi\rangle\), then \(B\) is the inverse of \(A\), and we write \(B=A^{-1}\). An operator that has an inverse is called invertible. Another important property that an operator may possess is positivity. An operator is positive if

\[\langle\phi|A| \phi\rangle \geq 0 \quad \text { for all }|\phi\rangle\tag{1.17}\]

We also write this as \(A \geq 0\).

From the matrix representation of operators you can easily see that the operators themselves form a linear vector space:

1. \(A+B=B+A\),
2. \(A+(B+C)=(A+B)+C\),
3. \(a(A+B)=a A+a B\),
4. \((a+b) A=a A+b A\),
5. \(a(b A)=(a b) A\).

We can also define the operator norm \(\|A\|\) according to

\[\|A\|=\sqrt{\operatorname{Tr}\left(A^{\dagger} A\right)} \equiv \sqrt{\sum_{i j} A_{i j}^{*} A_{j i}},\tag{1.18}\]

which means that the linear vector space of operators is again a Hilbert space. The symbol Tr(.) denotes the trace of an operator, and we will return to this special operator property later in this section.

Every operator has a set of vectors for which

\[A\left|a_{j}\right\rangle=a_{j}\left|a_{j}\right\rangle, \quad \text { with } a_{j} \in \mathbb{C}\tag{1.19}\]

This is called the eigenvalue equation (or eigenequation) for \(A\), and the vectors \(\left|a_{j}\right\rangle\) are the eigenvectors. The complex numbers \(a_{j}\) are eigenvalues. In the basis of eigenvectors, the matrix representation of \(A\) becomes

\[A=\left(\begin{array}{cccc}
a_{1} & 0 & \cdots & 0 \\
0 & a_{2} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & a_{N}
\end{array}\right)\tag{1.20}\]

When some of the \(a_{j} \mathrm{s}\) are the same, we speak of degenerate eigenvalues. When there are \(n\) identical eigenvalues, we have \(n\)-fold degeneracy. The eigenvectors corresponding to this eigenvalue then span an \(n\)-dimensional subspace of the vector space. We will return to subspaces shortly, when we introduce projection operators.

For any orthonormal basis \(\left\{\left|\phi_{j}\right\rangle\right\}_{j}\) we have

\[\left\langle\phi_{j}|A| \phi_{k}\right\rangle=A_{j k}\tag{1.21}\]

which can be written in the form

\[A=\sum_{j k} A_{j k}\left|\phi_{j}\right\rangle\left\langle\phi_{k}\right|\tag{1.22}\]

For the special case where \(\left|\phi_{j}\right\rangle=\left|a_{j}\right\rangle\) this reduces to

\[A=\sum_{j} a_{j}\left|a_{j}\right\rangle\left\langle a_{j}\right|\tag{1.23}\]

This is the spectral decomposition of \(A\). When all \(a_{j}\) are equal, we have complete degeneracy over the full vector space, and the operator becomes proportional (up to a factor \(a_{j}\)) to the identity \(\mathbb{I}\).

Note that this is independent of the basis \(\left\{\left|a_{j}\right\rangle\right\}\). As a consequence, for any orthonormal basis \(\left\{\left|\phi_{j}\right\rangle\right\}\) we have

\[\mathbb{I}=\sum_{j}\left|\phi_{j}\right\rangle\left\langle\phi_{j}\right|\tag{1.24}\]

This is the completeness relation, and we will use this many times in our calculations.

Lemma

If two non-degenerate operators commute \(([A, B]=0)\), then they have a common set of eigenvectors.

Proof

Let \(A=\sum_{k} a_{k}\left|a_{k}\right\rangle\left\langle a_{k}\right|\) and \(B=\sum_{j k} B_{j k}\left|a_{j}\right\rangle\left\langle a_{k}\right|\). We can choose this without loss of generality: we write both operators in the eigenbasis of \(A\). Furthermore, \([A, B]=0\) implies that \(A B=B A\).

\[\begin{aligned}
&A B=\sum_{k l m} a_{k} B_{l m}|a_{k}\rangle\langle a_{k} \mid a_{l}\rangle\langle a_{m}|=\sum_{l m} a_{l} B_{l m}| a_{l}\rangle\langle a_{m}| \\
&B A=\sum_{k l m} a_{k} B_{l m}|a_{l}\rangle\langle a_{m} \mid a_{k}\rangle\langle a_{k}|=\sum_{l m} a_{m} B_{l m}| a_{l}\rangle\left\langle a_{m}\right|
\end{aligned}\tag{1.25}\]

Therefore

\[[A, B]=\sum_{l m}\left(a_{l}-a_{m}\right) B_{l m}\left|a_{l}\right\rangle\left\langle a_{m}\right|=0\tag{1.26}\]

If \(a_{l} \neq a_{m}\) for \(l \neq m\), then \(B_{l m}=0\), and \(B_{l m} \propto \delta_{l m}\). Therefore \(\left\{\left|a_{j}\right\rangle\right\}\) is an eigenbasis for B.

The proof of the converse is left as an exercise. It turns out that this is also true when \(A\) and/or \(B\) are degenerate.