13.4: Quantized Energy Levels in Bound Systems

Last updated
Save as PDF

Page ID: 56888

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Whereas a free particle has a continuum of energy states available to it, if the particle is bound in a potential its available energy states are quantized. For a particle to be bound in a potential, the potential must limit a region of space that the particle could access classically. That is, if there is an energy well of some depth, the particle’s energy over the bottom of the well must be less than the depth of the well:

Screen Shot 2021-12-07 at 12.44.45 AM.png — A finite square potential well, with potential energy 0 chosen to be the bottom of the well. (Sometimes, one chooses the top of the well to be potential energy 0.) If a particle’s total energy is less than the depth of the well \(V_{0}\), as is the case for energy \(E_{1}\) in the figure, that particle is bound in the well. If the particle’s total energy is greater than the depth of the well, as is the case for energy \(E_{2}\) in the figure, that particle is free, although its wave function is still influenced by the presence of the well.

In this example, a particle would be classically limited to the range of position \(x_{0}<x<x_{1}\) (see Section 2.2.2). Quantum mechanically, the particle is most likely to be found in that range, but it turns out there is a finite non-zero probability that the particle is found outside the classically allowed volume!

In this square well, there are a finite number of energy states available to a particle. Classically, a bound particle could have any energy \(0 \leq E<V_{0}\). However, quantum mechanically, the particle must be in one of specific separated states. This is analogous to what we’ve seen with angular momentum of a spin-1/2 particle, where the projection of angular momentum along one axis must take on one of two specific separated values. For the square well, the allowed energy levels qualitatively looks something like:

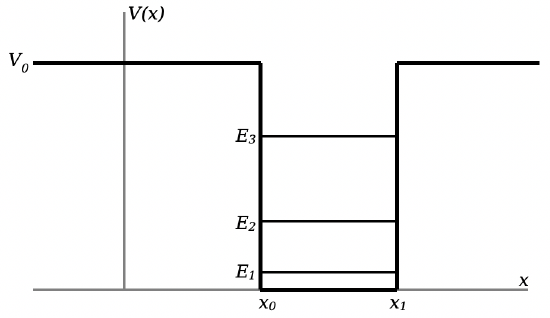
Screen Shot 2021-12-07 at 12.50.47 AM.png

In this example, there are only three allowed energy states, and the energies of those states are \(E_{1}\), \(E_{2}\), and \(E_{3}\). Notice that the lowest allowed energy level is not 0! That is, you can’t have a particle that’s got no kinetic energy. This fits with the Heisenberg Uncertainty Principle. By binding the particle into the potential well, you’ve set constraints on the particle’s position: it’s most likely to be between \(x_{0}\) and \(x_{1}\). The particle isn’t equally probable to be anywhere, so the uncertainty on the particle’s position \(\Delta x\) is finite (and indeed will be something close to \(x_{1}-x_{0}\)). As such, there must be a corresponding uncertainty in the particle’s momentum \(\Delta p\), so it’s impossible for the particle to be in a zero-momentum state.