2.5: Photoelectric Effect
( \newcommand{\kernel}{\mathrm{null}\,}\)
The so-called photoelectric effect, by which a polished metal surface emits electrons when illuminated by visible and ultra-violet light, was discovered by Heinrich Hertz in 1887 . The following facts regarding this effect can be established via careful observation. First, a given surface only emits electrons when the frequency of the light with which it is illuminated exceeds a certain threshold value, which is a property of the metal. Second, the current of photoelectrons, when it exists, is proportional to the intensity of the light falling on the surface. Third, the energy of the photoelectrons is independent of the light intensity, but varies linearly with the light frequency. These facts are inexplicable within the framework of classical physics.
In 1905, Albert Einstein proposed a radical new theory of light in order to account for the photoelectric effect . According to this theory, light of fixed frequency ν consists of a collection of indivisible discrete packages, called quanta,1 whose energy is
Suppose that the electrons at the surface of a metal lie in a potential well of depth W. In other words, the electrons have to acquire an energy W in order to be emitted from the surface. Here, W is generally called the work function of the surface, and is a property of the metal. Suppose that an electron absorbs a single quantum of light. Its energy therefore increases by hν. If hν is greater than W then the electron is emitted from the surface with residual kinetic energy K=hν−W.
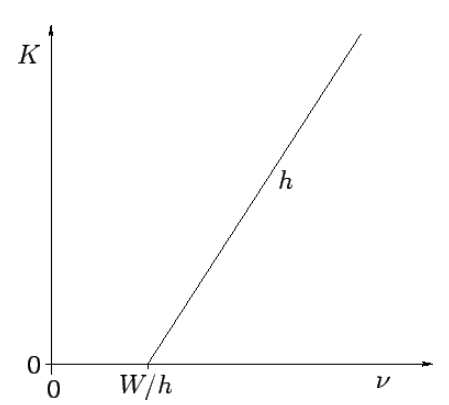
Figure 4: Variation of the kinetic energy ![]() of photoelectrons with the wave-frequency
of photoelectrons with the wave-frequency ![]() .
.
Contributors and Attributions
Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)


