8.6: Exercise Problems

8.1. Prove that Eq. (30) indeed yields \(E_{\mathrm{g}}{ }^{(1)}=(5 / 4) E_{\mathrm{H}}\).

8.2. For a dilute gas of helium atoms in their ground state, with \(n\) atoms per unit volume, calculate its:

(i) electric susceptibility \(\chi_{\mathrm{e}}\), and

(ii) magnetic susceptibility \(\chi_{\mathrm{m}}\),

and compare the results.

Hint: You may use the model solution of Problems \(6.8\) and \(6.14\), and the results of the variational description of the helium atom’s ground state in Sec. 2 .

8.3. Calculate the expectation values of the following observables: \(\mathbf{s}_{1} \cdot \mathbf{s}_{2}, S^{2} \equiv\left(\mathbf{s}_{1}+\mathbf{s}_{2}\right)^{2}\), and \(S_{z} \equiv\) \(s_{1 z}+s_{2 z}\), for the singlet and triplet states of the system of two spins-1/2, defined by Eqs. (18) and (21), directly, without using the general Eq. (48). Compare the results with those for the system of two classical geometric vectors of length \(\hbar / 2\) each.

8.4. Discuss the factors \(\pm 1 / \sqrt{2}\) that participate in Eqs. (18) and (20) for the entangled states of the system of two spins-1/2, in terms of Clebsh-Gordan coefficients similar to those discussed in Sec. 5.7.

8.5. \({ }^{*}\) Use the perturbation theory to calculate the contribution into the so-called hyperfine splitting of the ground energy of the hydrogen atom, \({ }^{100}\) due to the interaction between the spins of its nucleus (proton) and electron.

Hint: The proton’s magnetic moment operator is described by the same Eq. (4.115) as the electron, but with a positive gyromagnetic factor \(\gamma_{\mathrm{p}}=g_{\mathrm{p}} e / 2 m_{\mathrm{p}} \approx 2.675 \times 10^{8} \mathrm{~s}^{-1} \mathrm{~T}^{-1}\), whose magnitude is much smaller than that of the electron \(\left(\left|\gamma_{\mathrm{e}}\right| \approx 1.761 \times 10^{11} \mathrm{~s}^{-1} \mathrm{~T}^{-1}\right)\), due to the much higher mass, \(m_{\mathrm{p}} \approx\) \(1.673 \times 10^{-27} \mathrm{~kg} \approx 1,835 m_{\mathrm{e}}\). (The \(g\)-factor of the proton is also different, \(g_{\mathrm{p}} \approx 5.586 .{ }^{101}\) )

8.6. In the simple case of just two similar spin-interacting particles, distinguishable by their spatial location, the famous Heisenberg model of ferromagnetism \(^{102}\) is reduced to the following Hamiltonian: \[H=-J \hat{\mathbf{s}}_{1} \cdot \hat{\mathbf{s}}_{2}-\gamma \mathscr{B} \cdot\left(\hat{\mathbf{s}}_{1}+\hat{\mathbf{s}}_{2}\right),\] where \(J\) is the spin interaction constant, \(\gamma\) is the gyromagnetic ratio of each particle, and \(\mathscr{B}\) is the external magnetic field. Find the stationary states and energies of this system for spin- \(1 / 2\) particles.

8.7. Two particles, both with spin- \(1 / 2\) but different gyromagnetic ratios \(\gamma_{1}\) and \(\gamma_{2}\), are placed to external magnetic field \(\mathscr{B}\). In addition, their spins interact as in the Heisenberg model: \[\hat{H}_{\text {int }}=-J \hat{\mathbf{s}}_{1} \cdot \hat{\mathbf{s}}_{2} .\] Find the eigenstates and eigenenergies of the system.

8.8. Two similar spin- \(1 / 2\) particles, with gyromagnetic ratio \(\gamma\), localized at two points separated by distance \(a\), interact via the field of their magnetic dipole moments. Calculate stationary states and energies of the system.

8.9. Consider the permutation of two identical particles, each of spin \(s\). How many different symmetric and antisymmetric spin states can the system have?

8.10. For a system of two identical particles with \(s=1\) :

(i) List all spin states forming the uncoupled-representation basis.

(ii) List all possible pairs \(\left\{S, M_{S}\right\}\) of the quantum numbers describing the states of the coupledrepresentation basis - see Eq. (48).

(iii) Which of the \(\left\{S, M_{S}\right\}\) pairs describe the states symmetric, and which the states antisymmetric, with respect to the particle permutation?

8.11. Represent the operators of the total kinetic energy and the total orbital angular momentum of a system of two particles, with masses \(m_{1}\) and \(m_{2}\), as combinations of terms describing the center-ofmass motion and the relative motion. Use the results to calculate the energy spectrum of the so-called positronium - a metastable "atom" 103 consisting of one electron and its positively charged antiparticle, the positron.

8.12. Two particles with similar masses \(m\) and charges \(q\) are free to move along a round, plane ring of radius \(R\). In the limit of strong Coulomb interaction of the particles, find the lowest eigenenergies of the system, and sketch the system of its energy levels. Discuss possible effects of particle indistinguishability.

8.13. Low-energy spectra of many diatomic molecules may be well described by modeling the molecule as a system of two particles connected with a light and elastic, but very stiff spring. Calculate the energy spectrum of a molecule within this model. Discuss possible effects of nuclear spins on spectra of the so-called homonuclear diatomic molecules, formed by two similar atoms.

8.14. Two indistinguishable spin- \(-1 / 2\) particles are attracting each other at contact: \[U\left(x_{1}, x_{2}\right)=-w \delta\left(x_{1}-x_{2}\right), \quad \text { with } w>0,\] but are otherwise free to move along the \(x\)-axis. Find the energy and the orbital wavefunction of the ground state of the system.

8.15. Calculate the energy spectrum of the system of two identical spin- \(1 / 2\) particles, moving along the \(x\)-axis, which is described by the following Hamiltonian: \[\hat{H}=\frac{\hat{p}_{1}^{2}}{2 m_{0}}+\frac{\hat{p}_{2}^{2}}{2 m_{0}}+\frac{m_{0} \omega_{0}^{2}}{2}\left(x_{1}^{2}+x_{2}^{2}+\varepsilon x_{1} x_{2}\right),\] and the degeneracy of each energy level.

8.16. \({ }^{*}\) Two indistinguishable spin- \(1 / 2\) particles are confined to move around a circle of radius \(R\), and interact only at a very short arc distance \(l=R \varphi \equiv R\left(\varphi_{1}-\varphi_{2}\right)\) between them, so that the interaction potential \(U\) may be well approximated with a delta function of \(\varphi\). Find the ground state and its energy, for the following two cases:

(i) the "orbital" (spin-independent) repulsion: \(\hat{U}=w \delta(\varphi)\),

(ii) the spin-spin interaction: \(\hat{U}=-w \hat{\mathbf{s}}_{1} \cdot \hat{\mathbf{s}}_{2} \delta(\varphi)\),

both with constant \(w>0\). Analyze the trends of your results in the limits \(w \rightarrow 0\) and \(w \rightarrow \infty\).

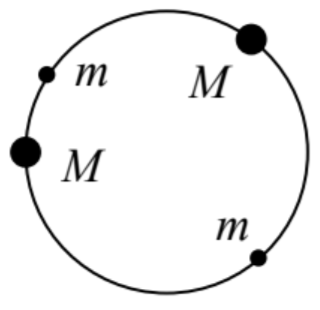
8.17. Two particles of mass \(M\), separated by two much lighter particles of mass \(m<<M\), are placed on a ring of radius \(R-\) see the figure on the right. The particles strongly repulse at contact, but otherwise, each of them is free to move along the ring. Calculate the lower part of the energy spectrum of the system.

8.18. \(N\) indistinguishable spin- \(-1 / 2\) particles move in a spherically-symmetric quadratic potential \(U(\mathbf{r})=m \omega_{0}^{2} r^{2} / 2\). Neglecting the direct interaction of the particles, find the ground-state energy of the system.

8.19. Use the Hund rules to find the values of the quantum numbers \(L, S\), and \(J\) in the ground states of the atoms of carbon and nitrogen. Write down the Russell-Saunders symbols for these states.

8.20. N \gg 1\) indistinguishable, non-interacting quantum particles are placed in a hard-wall, rectangular box with sides \(a_{x}, a_{y}\), and \(a_{z}\). Calculate the ground-state energy of the system, and the average forces it exerts on each face of the box. Can we characterize the forces by certain pressure \(\mathcal{P}\) ?

Hint: Consider separately the cases of bosons and fermions.

8.21. { }^{*}\) Explore the Thomas-Fermi model 104 of a heavy atom, with the nuclear charge \(Q=Z e \gg\) \(e\), in which the interaction between electrons is limited to their contribution to the common electrostatic potential \(\phi(\mathbf{r})\). In particular, derive the ordinary differential equation obeyed by the radial distribution of the potential, and use it to estimate the effective radius of the atom.

8.22. Use the Thomas-Fermi model, explored in the previous problem, to calculate the total binding energy of a heavy atom. Compare the result with that for the simpler model, in that the Coulomb electron-electron interaction is completely ignored.

8.23. A system of three similar spin- \(1 / 2\) particles is described by the Heisenberg Hamiltonian (cf. Problems 6 and 7): \[\hat{H}=-J\left(\hat{\mathbf{s}}_{1} \cdot \hat{\mathbf{s}}_{2}+\hat{\mathbf{s}}_{2} \cdot \hat{\mathbf{s}}_{3}+\hat{\mathbf{s}}_{3} \cdot \hat{\mathbf{s}}_{1}\right),\] where \(J\) is the spin interaction constant. Find the stationary states and energies of this system, and give an interpretation of your results.

8.24. For a system of three spins- \(1 / 2\), find the common eigenstates and eigenvalues of the operators \(\hat{S}_{z}\) and \(\hat{S}^{2}\), where \[\hat{\mathbf{S}} \equiv \hat{\mathbf{s}}_{1}+\hat{\mathbf{s}}_{2}+\hat{\mathbf{s}}_{3}\] is the vector operator of the total spin of the system. Do the corresponding quantum numbers \(S\) and \(M_{S}\) obey Eqs. (48)?

8.25. Explore basic properties of the Heisenberg model (which was the subject of Problems 6,7 , and 23), for a 1D chain of \(N\) spins-1/2: \[\hat{H}=-J \sum_{\{j, j\}} \hat{\mathbf{s}}_{j} \cdot \hat{\mathbf{s}}_{j^{\prime}}-\gamma \mathscr{B} \cdot \sum_{j} \hat{\mathbf{s}}_{j}, \quad \text { with } J>0,\] where the summation is over all \(N\) spins, with the symbol \(\left\{j, j^{\prime}\right\}\) meaning that the first sum is only over the adjacent spin pairs. In particular, find the ground state of the system and its lowest excited states in the absence of external magnetic field \(\mathscr{R}\), and also the dependence of their energies on the field.

Hint: For the sake of simplicity, you may assume that the first sum includes the term \(\hat{\mathbf{s}}_{N} \cdot \hat{\mathbf{s}}_{1}\) as well. (Physically, this means that the chain is bent into a closed loop. \({ }^{105}\) )

8.26. Compose the simplest model Hamiltonians, in terms of the second quantization formalism, for systems of indistinguishable particles moving in the following external potentials:

(i) two weakly coupled potential wells, with on-site particle interactions (giving additional energy \(J\) per each pair of particles in the same potential well), and

(ii) a periodic 1D potential, with the same particle interactions, in the tight-binding limit.

8.27. For each of the Hamiltonians composed in the previous problem, derive the Heisenberg equations of motion for particle creation/annihilation operators:

(i) for bosons, and

(ii) for fermions.

8.28. Express the ket-vectors of all possible Dirac states for the system of three indistinguishable

(i) bosons, and

(ii) fermions,

via those of the single-particle states \(\beta, \beta^{\prime}\), and \(\beta^{\prime \prime}\) they occupy.

8.29. Explain why the general perturbative result (8.126), when applied to the \({ }^{4} \mathrm{He}\) atom, gives the correct \(^{106}\) expression (8.29) for the ground singlet state, and correct Eqs. (8.39)-(8.42) (with the minus sign in the first of these relations) for the excited triplet states, but cannot describe these results, with the plus sign in Eq. (8.39), for the excited singlet state.

8.30. For a system of two distinct qubits (i.e. two-level systems), introduce a reasonable uncoupled-representation \(z\)-basis, and write in this basis the \(4 \times 4\) matrix of the operator that swaps their states.

8.31. Find a time-independent Hamiltonian that can cause the qubit evolution described by Eqs. (155). Discuss the relation between your result and the time-dependent Hamiltonian (6.86).

---

\({ }^{100}\) This effect was discovered experimentally by A. Michelson in 1881 and explained theoretically by W. Pauli in \(1924 .\)

\({ }^{101}\) The anomalously large value of the proton’s \(g\)-factor results from the composite quark-gluon structure of this particle. (An exact calculation of \(g_{\mathrm{p}}\) remains a challenge for quantum chromodynamics.)

\({ }_{102}\) It was suggested in 1926, independently by W. Heisenberg and P. Dirac. A discussion of thermal motion effects on this and other similar systems (especially the Ising model of ferromagnetism) may be found in SM Chapter \(4 .\)

\({ }^{103}\) Its lifetime (either \(0.124 \mathrm{~ns}\) or \(138 \mathrm{~ns}\), depending on the parallel or antiparallel configuration of the component spins), is limited by the weak interaction of its components, which causes their annihilation with the emission of several gamma-ray photons.

\({ }^{104}\) It was suggested in 1927 , independently, by L. Thomas and E. Fermi.

\({ }^{105}\) Note that for dissipative spin systems, differences between low-energy excitations of open-end and closed-end 1D chains may be substantial even in the limit \(N \rightarrow \infty-\) see, e.g., SM Sec. 4.5. However, for our Hamiltonian (and hence dissipation-free) system, the differences are relatively small.

\({ }^{106}\) Correct in the sense of the first order of the perturbation theory.