3.1: How can they both . . . ?
- Page ID
- 3432
Learning Objectives
- Who is really slow?
Figure \(\PageIndex{1}\) shows how relativity resolves the first question. If \(A\) and \(B\) had an instantaneous method of communication such as Star Trek’s subspace radio, then they could indeed resolve the question of who was really slow.
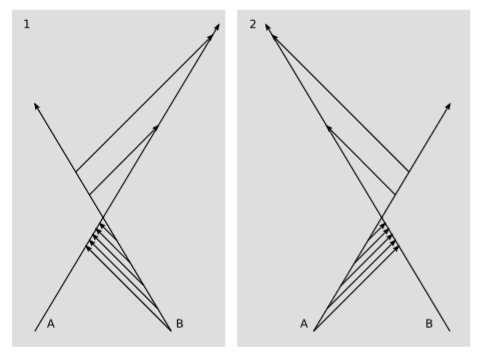
But relativity does not allow cause and effect to be propagated outside the light cone, so the best they can actually do is to send each other signals at \(c\). In figure \(\PageIndex{1}\) (1), \(B\) sends signals to \(A\) at time intervals of one hour as measured by \(B\)’s clock. According to \(A\)’s clock, the signals arrive at an interval that is shorter than one hour as the two spaceships approach one another, then longer than an hour after they pass each other and begin to recede. As shown in figure \(\PageIndex{1}\) (2), the situation is entirely symmetric if \(A\) sends signals to \(B\).
Who is really slow? Neither. If \(A\), like many astronauts, cut her teeth as a jet pilot, it may occur to her to interpret the observations by analogy with the Doppler effect for sound waves. Figure \(\PageIndex{1}\) is in fact a valid diagram if the signals are clicks of sound, provided that we interpret it as being drawn in the frame of reference of the air. Sound waves travel at a fixed speed relative to the air, and the space and time units could be chosen such that the speed of sound was represented by a slope of \(\pm 1\). But \(A\) will find that in the relativistic case, with signals traveling at \(c\), her observations of the time intervals are not in quantitative agreement with the predictions she gets by plugging numbers into the familiar formulas for the Doppler shift of sound waves. She may then say, “Ah, the analogy with sound isn’t quite right. I need to include a correction factor for time dilation, since B’s time is slow. I’m not slow, of course. I feel perfectly normal.”
But her analogy is false and needlessly complicates the situation. In the version with sound waves and Galilean relativity, there are three frames of reference involved: \(A\)’s, \(B\)’s, and the air’s. The relativistic version is simpler, because there are only two frames, \(A\)’s and \(B\)’s. It’s neither helpful nor necessary to break down the observations into a factor describing what “really” happens and a correction factor to account for the relativistic distortions of “reality.” All we need to worry about is the world-lines and intersections of worldlines shown in the spacetime diagrams, along with the metric, which allows us to compute how much proper time is experienced by each observer.


