3.2: The stretch factor is the Doppler shift
- Page ID
- 3433
Learning Objectives
- Explain the Doppler shift
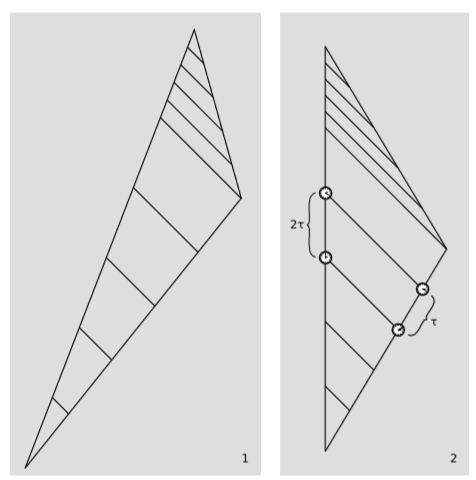
Figure \(\PageIndex{1}\) shows how the ideas in the preceding section apply to the twin paradox. In figure \(\PageIndex{1}\) (1) we see the situation as described by an impartial observer, who says that both twins are traveling to the right. But even the impartial observer agrees that one twin’s motion is inertial and the other’s noninertial, which breaks the symmetry and also allows the twins to meet up at the end and compare clocks. For convenience, figure \(\PageIndex{1}\) (2) shows the situation in the frame where the earthbound twin is at rest. Both panels of the figure are drawn such that the relative velocity of the twins is \(3/5\), and in panel \(2\) this is the inverse slope of the traveling twin’s world-lines. Straightforward algebra and geometry (problem Q6) shows that in this particular example, the period observed by the earthbound twin is increased by a factor of \(2\). But \(2\) is exactly the factor by which the diagonals of the parallelogram are stretched and compressed in a Lorentz transformation for a velocity of \(3/5\). This is true in general: the stretching and squishing factors for the diagonals are the same as the Doppler shift. We notate this factor as \(D\) (which can stand for either “Doppler” or “diagonal”), and in general it is given by
\[D(v) = \sqrt{\dfrac{1+v}{1-v}}\]
Exercise \(\PageIndex{1}\)
If you measure with a ruler on figure \(\PageIndex{1}\) (2), you will find that the labeled sides of the quadrilateral differ by less than a factor of \(2\). Why is this?
This expression is for the longitudinal Doppler shift, i.e., the case where the source and observer are in motion directly away from one another (or toward one another if \(v < 0\)). In the purely transverse case, there is a Doppler shift \(1/\gamma\) which can be interpreted as simply a measure of time dilation.
The useful identity \(D(v)D(-v) = 1\) is trivial to prove algebraically, and has the following interpretation.

Suppose, as in figure \(\PageIndex{2}\), that \(A\) and \(C\) are at rest relative to one another, but \(B\) is moving relative to them. \(B\)’s velocity relative to \(A\) is \(v\), and \(C\)’s relative to \(B\) is \(-v\). At regular intervals, \(A\) sends lightspeed “pings” to \(B\), who then immediately retransmits them to \(C\). The interval between pings accumulates two Doppler shifts, and the result is their product \(D(v)D(-v)\). But \(B\) didn’t actually need to receive the original signal and retransmit it; the results would have been the same if \(B\) had just stayed out of the way. Therefore this product must equal \(1\), so \(D(v)D(-v) = 1\).
Example \(\PageIndex{1}\): Ives-Stilwell experiments
The transverse Doppler shift is a characteristic prediction of special relativity, with no nonrelativistic counterpart, and Einstein suggested it early on as a test of relativity. However, it is difficult to measure with high precision, because the results are sensitive to any error in the alignment of the \(90\)-degree angle. Such experiments were eventually performed, with results that confirmed relativity,1 but one-dimensional measurements provided both the earliest tests of the relativistic Doppler shift and the most precise ones to date. The first such test was done by Ives and Stilwell in 1938, using the following trick. The relativistic expression
\[D(v) = p (1 + v)/(1 − v)\]
for the Doppler shift has the property that \(D(v)D(-v) = 1\), which differs from the nonrelativistic result of
\[(1 + v)(1 − v) = 1 − v^2 \]
One can therefore accelerate an ion up to a relativistic speed, measure both the forward Doppler shifted frequency \(f_f\) and the backward one \(f_b\), and compute \(\sqrt{f_ff_b}\). According to relativity, this should exactly equal the frequency \(f_o\) measured in the ion’s rest frame. In a particularly exquisite modern version of the Ives-Stilwell idea,2 Saathoff et al. circulated \(Li+\) ions at \(v = 0.064\) in a storage ring. An electron-cooler technique was used in order to reduce the variation in velocity among ions in the beam. Since the identity \(D(v)D(-v) = 1\) is independent of \(v\), it was not necessary to measure \(v\) to the same incredible precision as the frequencies; it was only necessary that it be stable and well-defined. The natural line width was \(7\) MHz, and other experimental effects broadened it further to \(11\) MHz. By curve-fitting the line, it was possible to achieve results good to a few tenths of a MHz. The resulting frequencies, in units of MHz, were:
\[f_f = 582490203.44 \pm .09\\ f_b = 512671442.9 \pm 0.5\\ \sqrt{f_ff_b} = 546466918.6 \pm 0.3\\ f_o = 546466918.8 \pm 0.4 \text{(from previous experimental work)}\]
The spectacular agreement with theory has made this experiment a lightning rod for anti-relativity kooks. If one is searching for small deviations from the predictions of special relativity, a natural place to look is at high velocities. IvesStilwell experiments have been performed at velocities as high as \(0.84\), and they confirm special relativity.3
References
1 See, e.g., Hasselkamp, Mondry, and Scharmann, Zeitschrift fu¨r Physik A: Hadrons and Nuclei 289 (1979) 151.
2 G. Saathoff et al., “Improved Test of Time Dilation in Relativity,” Phys. Rev. Lett. 91 (2003) 190403. A publicly available description of the experiment is given in Saathoff’s PhD thesis, www.mpi-hd.mpg.de/ato/homes/saathoff/ diss-saathoff.pdf.
3 MacArthur et al., Phys. Rev. Lett. 56 (1986) 282 (1986)


