3.7: The Projection Operator
- Page ID
- 13035
Learning Objectives
- Explain the projection operator
A frequent source of confusion in relativity is that we write down equations that are coordinate-dependent, but forget the dependency. Similarly, it is possible to write expressions that are only valid for one choice of signature. The following notation, defining a projection operator \(P\), is one tool for avoiding these difficulties.
\[P_or = r - \dfrac{r\cdot o}{o\cdot o}o\]
Usually \(o\) is the future timelike vector representing a certain observer, but the definition can be applied as long as \(o\) isn’t lightlike. The idea being expressed is that we want to get rid of any part of \(r\) that is parallel to \(o\)’s arrow of time. In a graph constructed according to \(o\)’s Minkowski coordinates, we cast \(r\)’s shadow down perpendicularly onto the spacelike axis, or the spacelike three-plane in \(3+1\) dimensions. This is why \(P\) is referred to as a projection operator. The notation sometimes allows us to express the things that we would otherwise express by explicitly or implicitly constructing and referring to \(o\)’s spacelike Minkowski coordinates.
Properties of projection operator
\(P\) has the following properties:
- \(o\cdot P_or = 0\)
- \(r - P_or\) is parallel to \(o\).
- \(P_o o = 0\)
- \(P_o P_or = P_or\)
- \(P_{co} = P_o\)
- \(P_o\) is linear, i.e., \(P_o(q +r) = P_oq + P_or\) and \(P_o(cr) = cP_or\)
- \(\tfrac{d}{dx}P_or = P_o\tfrac{dr}{dx}\), where \(x\) is any variable and \(o\) doesn’t depend on \(x\).
- If \(o\) and \(v\) are both future timelike, and \(|o^2| = 1\), then we can express \(v\) as \(v = P_ov + \gamma o\), where \(\gamma\) has the usual interpretation for world-lines that coincide with these two vectors.
All of these hold regardless of whether the signature is \(+---\) or \(-+ ++\), and none of them refer to any coordinates. Properties 1 and 2 can serve as an alternative, geometrical definition of \(P\). Property 3 says that an observer considers herself to be at rest. Property 4 is a general property of all projection operators. Property 8 splits the vector into its spatial and temporal parts according to \(o\).
Sometimes if we know a position, velocity, or acceleration fourvector, we want to find out how these would be measured by a particular observer using clocks and rulers. The following table \(\PageIndex{1}\) shows how to switch back and forth between the two representations. We use, for example, the notation \(v_o\) to mean the velocity vector of the form \((0,v_x,v_y,v_z)\) that would be measured by an observer whose velocity vector is \(o\) (so that the subscript is an “\(o\)” for “observer,” not a zero). Since this type of vector, expressed in the Minkowski coordinates of observer \(o\), has a zero time component, we refer to it as a three-vector. In all of these expressions, the velocity vectors \(o\) and \(v\) are assumed to be normalized, and the signature is assumed to be \(+---\) (one implication being that \(o\cdot v\) is simply \(\gamma\)).
| Finding the three-vector from the four-vector | Finding the four-vector from the three-vector |
|---|---|
| \(X_o = P_oX\) | |
| \(v_o = \dfrac{P_ov}{o\cdot v}\) | \(v = \gamma (o + v_o)\) |
| \(a_o = \dfrac{1}{(o\cdot v)^2}\left [ P_oa - (o\cdot a)v_o \right ]\) | \(a = \gamma ^3(a_o\cdot v_o)v + \gamma ^2a_o\), where \(v\) is found as above |
As an example of how these are derived, the three-velocity \(v_o\) is the derivative of \(x_o\) with respect to observer \(o\)’s Minkowski time coordinate \(t\), whereas the four-velocity is defined as the derivative of \(x\) with respect to the proper time \(τ\) of the world-line being observed. Therefore we have
\[\begin{align*} v_o &= \dfrac{\mathrm{dX_o} }{\mathrm{d} t}\\[5pt] &= \dfrac{\mathrm{d} P_oX}{\mathrm{d} t} \end{align*}\]
and applying property 7 of the projection operator this becomes
\[\begin{align*} v_o &= P_o\dfrac{\mathrm{dX} }{\mathrm{d} t}\\[5pt] &= P_o\dfrac{\mathrm{d} X}{\mathrm{d} \tau }\dfrac{\mathrm{d} \tau }{\mathrm{d} t}\\[5pt] &= \dfrac{1}{\gamma }P_o\dfrac{\mathrm{d} X}{\mathrm{d} \tau }\\[5pt] &= \dfrac{1}{o\cdot v}P_o\dfrac{\mathrm{d} X}{\mathrm{d} \tau }\\[5pt] &= \dfrac{P_o v}{o\cdot v} \end{align*}\]
The similar but messier derivation of the expression for \(a_o\) is problem Q15. In manipulating expressions of this type, the identity \(\dfrac{\mathrm{d} \gamma }{\mathrm{d} t} = \gamma ^3 a_o\cdot v_o\) is often handy.
Example \(\PageIndex{1}\): Lewis-Tolman paradox
The following example is a form of a paradox discussed by Lewis and Tolman in 1909.
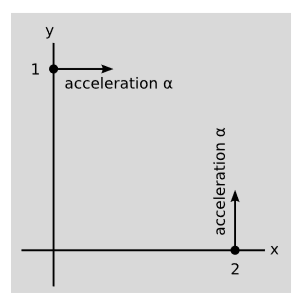
Figure \(\PageIndex{1}\) shows the frame of reference of observer \(o\) in which identical particles \(1\) and \(2\) are at initially rest and located at equal distances \(l\) from the origin along the \(y\) and \(x\) axes. External forces of equal strength act in the directions shown by the arrows so as to produce accelerations of magnitude \(α\). The system is in rotational equilibrium \(dL/dt = 0\), because the rate at which particle \(1\) picks up clockwise angular momentum is the same as the rate at which \(2\) acquires it in the counterclockwise direction.
Now change to the frame of reference o0, moving to the right relative to \(o\) at velocity \(v\). Particle \(2\)’s distance from the origin is Lorentz-contracted from \(l\) to \(l/\gamma\), so its angular momentum is also reduced by \(1/\gamma\). It now appears that the system’s total angular momentum is increasing in the clockwise sense. How can we have rotational equilibrium in one frame, but not another?
The resolution of the paradox is that the accelerations transform as well. In the original frame \(o\), the four-velocities are \(v_1 = v_2 = (1,0,0,0)\), and the four-accelerations are \(a_1 = (0,α,0,0)\) and \(a_2 = (0,0,α,0)\). Applying a Lorentz transformation, we have \(v_{1}^{'} = v_{2}^{'} = (\gamma ,-\gamma v,0,0)\) and
\[a_{1}^{'} = \alpha (-\gamma v,\gamma ,0,0)\\[5pt] a_{2}^{'} = \alpha (0,0,1,0) \nonumber\]
Our definition of angular momentum is expressed in terms of three-vectors such as \(a_{o'1}\) and \(a_{o'2}\), not four-vectors like \(a_{1}^{'}\) and \(a_{2}^{'}\). We have
\[\dfrac{\mathrm{d} L'}{\mathrm{d} t'} = ma_{o'1x}l - ma_{o'2y}\dfrac{l}{\gamma } \nonumber\]
Using the relations \(v_o = \gamma ^{-1}P_o v\) and \(a_o = \gamma ^{-2}\left [ P_o a - (o\cdot a)v_o\right ]\), we find
\[v_{o'1x} = -v\]
\[a_{o'1x} = \dfrac{1}{\gamma ^2}\left [ \alpha \gamma - (-\alpha \gamma v)(-v) \right ] = \dfrac{\alpha }{\gamma ^3} \nonumber\]
and
\[a_{o'2y} = \dfrac{\alpha }{\gamma ^2} \nonumber\]
The result is
\[\dfrac{\mathrm{d} L'}{\mathrm{d} t'} = m\dfrac{\alpha }{\gamma ^3}l - m\dfrac{\alpha }{\gamma ^2}\dfrac{l}{\gamma } \nonumber\]
which is zero.


