Life, Emerging Structures, and the Second Law of Thermodynamics
- Page ID
- 4116
Introduction
"A theory is the more impressive the greater the simplicity of its premises, the more varied the kinds of things that it relates and the more extended the area of its applicability. Therefore classical thermodynamics has made a deep impression on me. It is the only physical theory of universal content which I am convinced, within the areas of the applicability of its basic concepts, will never be overthrown." -- Einstein (1949)
This document investigates the emergence of structures, particularly living organisms, and the relationship of this process to the Second Law of Thermodynamics. The level is fairly elementary, and grew out of course notes for a liberal arts Physics course at the University of Toronto. The structure of the document is:
- A very brief overview of the Second Law of Thermodynamics. Further information on the Second Law of Thermodynamics is available here.
- A similarly brief overview of Chaos. Further details on this are available here.
- Discussion of systems in which order arises from disorder, despite the Second Law of Thermodynamics.
- An introduction to Cellular Automata.
- A discussion of evolution and maintenance of life on Earth.
Parts of this page and the pages it uses require Flash; the player is available free from http://www.macromedia.com/. Other parts use Java; the Java run time environment is available free from http://java.sun.com/.
Illustrating the Second Law of Thermodynamics
There are many many different equivalent ways of stating the Second Law of Thermodynamics. Here is one of them:
The total disorder of all the participants in any physical process "never" decreases, but it can increase.
The entropy is a measure of the disorder of a system. This definition can lead to confusion since it is a measure of the lack of order, while we usually think of physical quantities as measuring the presence of some property, not its lack. In fact, the negative of the entropy, the negentropy, is a measure of the order of the system. Here, then, are two more equivalent statements of the Second Law of Thermodynamics:
The total entropy of an isolated physical system "never" decreases.
The total negentropy of an isolated physical system "never" increases.
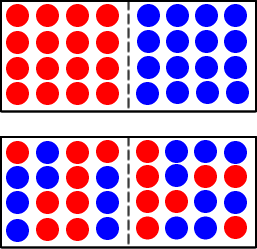 Here is an example. We say that the upper arrangement of the red and blue spheres is more ordered than the lower arrangement. The upper arrangement has all the red spheres on the left and all the blue ones on the right; the lower arrangement has the spheres randomly distributed between the left and right.
Here is an example. We say that the upper arrangement of the red and blue spheres is more ordered than the lower arrangement. The upper arrangement has all the red spheres on the left and all the blue ones on the right; the lower arrangement has the spheres randomly distributed between the left and right.
If we shake the box containing the spheres, we would expect to end up with an arrangement that looks more like the lower one than the upper one: the disorder of the system increases.
If we think of the red spheres as being hot molecules and the blue ones as cold molecules, then we see that if we start with the left side hot and the right side cold, the system will evolve into a state with equal temperature on the left and right side.
Clicking on the blue button to the right will illustrate the Second Law of Thermodynamics. The animation is in Flash, and will appear in a separate window. It is by Vera Fleischer ![]() and is used by permission.
and is used by permission.
The first part of the animation is an increase in disorder, and the second part is a decrease. The first part is what you might expect if you randomly shake the sentence and let the letters just arrange themselves wherever they wish. The second part is very very unlikely to happen spontaneously through some sort of shaking process.
You may wish to note that when the letters are arranged into the quote by Einstein, they contain information which we can read. When they are scrambled there is not anything readable. Thus the order, the negentropy, can be associated with information.
As you may know, the air in the room in which you're probably reading this has bazillions and bazillions of air molecules, all moving around in random directions, colliding with each other, etc. If all the molecules suddenly rushed up into the far corner by the ceiling, we would say they have become more ordered. But the chances of this happening, causing you to suffocate, is very very unlikely. In fact, since a bazillion is such a large number we can pretty well ignore the possibility of it happening. But since the probability of it happening is not exactly zero, I put the quotation marks around never.
Technical Note: a bazillion is defined to be a power of ten whose value is much much larger than 342.
Illustrating Chaos
In the late 17th century Newton triumphed and managed to use his newly formulated Laws of Dynamics and Law of Universal Gravitation to solve the problem of the Earth in orbit about a fixed Sun.
The Earth moves in a nearly circular orbit about the Sun.
Our Physics students learn to solve this system in their first year of studies.
 Newton then turned his attention to the second most simple gravitational problem: two fixed Suns and one Earth. He was amazed to discover that he could not solve it.
Newton then turned his attention to the second most simple gravitational problem: two fixed Suns and one Earth. He was amazed to discover that he could not solve it.
Others tried to solve this famous "three body problem" and also failed. At one point there was a cash prize for its solution.
It turns out that this system is chaotic and is not analytically solvable. However, computers can produce an approximate solution that is as close to correct as we wish to make it. Among the properties that this system, and all chaotic systems, possess is that it exhibits Sensitive Dependence on Initial Conditions. This is sometimes called the "butterfly effect" because if, say, history were chaotic then whether or not a particular butterfly landed on a particular flower in the Himalayan mountains in 1837 determined the outcome of World War II.
I have done a Flash animation of the solution to the three-body gravitational problem. In it you can have up to four non-interacting planets that begin with almost identical initial positions and speeds. As the animation progresses you can see that after a while the "orbits" radically diverge.
![]() The blue button to the right accesses the animation in a separate window. The number of planets is chosen in the lower-right corner of the window.
The blue button to the right accesses the animation in a separate window. The number of planets is chosen in the lower-right corner of the window.
Can Order Arise From Disorder?
 Consider a gravel road, such as are still common in many rural areas. The photograph to the right, taken by Donald Simanek of Lock Haven University of Pennsylvania in 2005, illustrates.
Consider a gravel road, such as are still common in many rural areas. The photograph to the right, taken by Donald Simanek of Lock Haven University of Pennsylvania in 2005, illustrates.
When first graded, crushed limestone of a variety sizes are laid down essentially randomly on the surface. And yet over time the road becomes rutted, the horizontal hills of stones and valleys of hard subsurface below, that can be seen in the photograph.
The ruts developed from traffic, especially near abrupt curves where cars had to brake to slow down. They were shallow at first but got rougher and deeper with time, and have a characteristic spacing.
This system, then, became more orderly as time went by. But this is not a violation of the Second Law of Thermodynamics, because that law only talks about the total entropy of a system that is not interacting with anything outside of it. Here the road is interacting with the traffic that causes the rutting. If we consider the total entropy of the gravel and the traffic, it will necessarily increase: the decrease in entropy of the gravel is more than matched by the increase in the cars and trucks traveling on the road.
 Here is a beautiful example, also from Prof. Simanek. It is a picture of sand dunes in the desert, and you can clearly see that the sand has ordered itself into ripples. These were caused by the wind blowing over the desert.
Here is a beautiful example, also from Prof. Simanek. It is a picture of sand dunes in the desert, and you can clearly see that the sand has ordered itself into ripples. These were caused by the wind blowing over the desert.
So here the increase in order of the sand was accompanied by a larger increase in the disorder of the wind.
Cellular Automata
Cellular automata provide another way to think about order and disorder. One of the best known automata is the Game of Life, devised by John Conway in 1970. This example is played on a large checkerboard-like grid. One starts with a configuration of cells on the board that are populated, and then calculates the population in succeeding generations using three simple rules:
- Birth: an unoccupied cell with exactly 3 occupied neighbors will be populated in the next generation.
- Survival: an occupied cell with 2 or 3 occupied neighbors will be populated in the next generation.
- Death: in all other cases a cell is unoccupied in the next generation.
Despite the simplicity of the rules, truly amazing patterns of movement, self-organising complexity, and more arise in this "game."
To the right is a Flash animation of the simplest possible configuration that changes from generation to generation but never grows or dies out. It is called a blinker.
- Click on the Step button to step from generation to generation. In this mode the number of occupied neighbors of each cell is shown.
- Click on Play to resume playing the animation.
 Here is a small taste of some of the things that can happen in this game. This example is Gosper's "Glider Gun" and this implementation of it is from Wikipedia.
Here is a small taste of some of the things that can happen in this game. This example is Gosper's "Glider Gun" and this implementation of it is from Wikipedia.
Every 30 generations a glider is generated and travels to the lower-right.
You should be aware that this sort of behavior did not arise just by accident. The initial state leading to this behavior was carefully crafted in 1970 by R. William Gosper, Jr., and several student colleagues at M.I.T. It won a $50 prize offered by Conway as the first known infinitely growing pattern.
The pattern, the glider, moves. But the squares are just becoming occupied or unoccupied; they are not moving.
You may wish to notice that in this implementation, when a glider goes out of the picture it simply disappears. Other variations of the Game of Life have an object that disappears on one side of the window wrap around and re-appear on the opposite side.
![]() Clicking on the blue button to the right will access a Java implementation of the Glider Gun that has this "wraparound" property. It will appear in a separate window. This implementation is by Mitchel Resnick and Brian Silverman at M.I.T.
Clicking on the blue button to the right will access a Java implementation of the Glider Gun that has this "wraparound" property. It will appear in a separate window. This implementation is by Mitchel Resnick and Brian Silverman at M.I.T.
We have seen that the Glider Gun generates ordered gliders every 30 generations, and that the generation process is chaotic: it exhibits the butterfly effect.
This system does not violate the Second Law of Thermodynamics. Imagine that, like Conway in 1970, we are playing the game on a checker board (actually Conway used a Go board). If we just shake the board to reposition the pieces, then clearly the system of board and pieces are not isolated, so the Second Law does not apply.
There is an added part of this story however. If we just shake the board the rules for where the pieces will land is just classical mechanics, and the number of pieces is constant unless some fall off the board. But in the Game of Life different rules govern which cells will be occupied in the next generation.
Also, the Glider Gun shows that unpopulating a single occupied square or populating a single unoccupied one often leads to drastic changes in the time evolution of the system. This is reminiscent of the Sensitive Dependence on Initial Conditions that characterizes all chaotic systems. You may also recall that non-chaotic systems become chaotic as some parameter describing the system changes, and in fact the Glider Gun is right on the edge of being a true chaotic system.
There are many different rules that are used in the study of these cellular automata. One well known rule set is by Brian Silverman and is called Brian's Brain. The rules are:
- Birth: an unoccupied cell with exactly two occupied neighbors will by populated in the next generation.
- Death: every occupied cell dies in the next generation.
- Rest: if an occupied cell dies it must wait one generation before it can be populated.
![]() Clicking on the blue button to the right will access a Java implementation of Brian's Brain in a separate window. This is also by Mitchel Resnick and Brian Silverman at M.I.T.
Clicking on the blue button to the right will access a Java implementation of Brian's Brain in a separate window. This is also by Mitchel Resnick and Brian Silverman at M.I.T.
We see that although glider generation in Life requires a carefully controlled initial state, the Brian's Brain rule set makes it very difficult to avoid making gliders.
Recently a rule set called Rule 110 has been receiving a lot of attention. One starts with a pattern on a row, and the rules determine the population of the row under the current one in the next generation. The rules are given below, and the Flash animation to the right illustrates for a starting configuration of a single occupied cell. In the rule table below a 1 indicates a populated cell; a 0 indicates an empty cell.
| current pattern | 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
| new state for center cell | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
In the 1990's Matthew Cook proved that such a rule set can be a model of any computer.
 To the right is an more complete but non-animated example of Rule 110 for a starting configuration of a single occupied cell. The figure is from Wikipedia.
To the right is an more complete but non-animated example of Rule 110 for a starting configuration of a single occupied cell. The figure is from Wikipedia.
It has been proposed that cellular automata may form a useful model for how the universe really works, possibly supplanting Physics. We've already mentioned some people; other contributors to this idea include Konrad Zuse in 1967, Edward Fredkin in the early 1980's, and more recently Stephen Wolfram in 2002. Wolfram's work in particular is the outcome of nearly a decade of work, which is described in a mammoth 1200 page self-published book modestly titled A New Kind of Science.
Evolution and Sustaining Life on Earth
Warning: at the end of this section I will indulge in some ranting and raving about energy sources.
A vivarium is a sealed ecosystem. A large clear container has some soil, water, plants, perhaps some snails, etc. in carefully controlled proportions placed inside. The container is then totally sealed and placed in the sunlight. This ecosystem can survive for a long long time with no maintenance required. In fact, with care a vivarium can be constructed that initially increases the total amount of biomass inside until it reaches a steady state. What does the Second Law of Thermodynamics say about this? That there is no problem: although the system cannot exchange matter with the outside, energy from the sunlight is streaming through the ecosystem so it is not really closed. If you place the vivarium in a dark closet, the Second Law will take over and very soon you will have a high-entropy foul-smelling goo of decomposed biomass.
We can think of the Earth as being very similar to the vivarium. The exchange of matter between the Earth and space is fairly negligible, but energy from the sunlight is streaming through the system. In fact during the day about 1400 Joules per second (nearly 2 horsepower) reaches every square meter of the Earth's surface. A similar quantity of energy is radiated away into space from the Earth as thermal radiation.
Millions of years ago the Earth had no life and had a relatively high entropy. Now life has evolved, and the Earth contains about a trillion kilograms of ordered low-entropy biomass. And this all occurred because of the energy from the Sun that streams through the Earth's system. The rule set that governs this process is given by physics, chemistry, biology, and evolution.
This is not the appropriate place to discuss evolution, which I believe to be a fact.
Now let's consider some energy sources that we use.
1. Solar Panels and Heaters
 Solar panels directly convert sunlight to electrical energy. In addition, in many parts of the world the majority of hot water heaters are on the roofs of the houses and use sunlight directly to heat the water.
Solar panels directly convert sunlight to electrical energy. In addition, in many parts of the world the majority of hot water heaters are on the roofs of the houses and use sunlight directly to heat the water.
My uncle was fond of talking about my aunt's solar powered clothes dryer: a common clothes line strung between the house and a convenient nearby tree.
This photograph is by David Anderson, and is in the public domain.
2. Hydroelectric Power
 We build dams that extract energy from water that is flowing downhill. But how did the water get on top of hill? The heat from the Sun evaporated the water in the oceans and lakes, and rain then deposited some of it on top of the hills and mountains. Thus hydroelectric power is generated from solar power.
We build dams that extract energy from water that is flowing downhill. But how did the water get on top of hill? The heat from the Sun evaporated the water in the oceans and lakes, and rain then deposited some of it on top of the hills and mountains. Thus hydroelectric power is generated from solar power.
The photograph is of the Grand Canyon dam. It was taken by Steven Pinker at Harvard, and is used by permission.
3. Wind Power
 Wind turbines and windmills extract energy from the wind. But what causes the wind? The sun heats up the air in tropical regions, which causes it to rise. Near the poles the air cools down and falls. So there is a continual circulation of air rising near the equator, traveling north and south high above the Earth's surface, falling nearer to the surface near the poles, and traveling back to the tropical regions nearer the surface. The fact that the Earth is rotating on its axis causes the wind to swirl, but the energy of the wind is also solar.
Wind turbines and windmills extract energy from the wind. But what causes the wind? The sun heats up the air in tropical regions, which causes it to rise. Near the poles the air cools down and falls. So there is a continual circulation of air rising near the equator, traveling north and south high above the Earth's surface, falling nearer to the surface near the poles, and traveling back to the tropical regions nearer the surface. The fact that the Earth is rotating on its axis causes the wind to swirl, but the energy of the wind is also solar.
The photograph is of the wind turbine at Exhibition Place in Toronto.
4. Biomass
 We extract energy from biomass in a variety of ways. This includes burning wood, possibly to run a steam engine, extracting ethanol from it, etc.
We extract energy from biomass in a variety of ways. This includes burning wood, possibly to run a steam engine, extracting ethanol from it, etc.
Or course, the energy got into the biomass from sunlight, so this too is solar power.
These energy sources are all sustainable and renewable. In the language we have been using in this document, this means that they treat the Earth as an open system and thus allow our low-entropy ecosystem to survive and prosper.
Let us continue thinking about energy sources.
5. Petroleum, Coal, Natural Gas. These energy sources are also ultimately from the Sun: biomass from hundreds of thousands of years ago became trapped in the Earth as oil, coal and gas deposits. However, these energy sources are not renewable: they are no longer being produced. Thus they all treat the Earth as a closed system. The Second Law of Thermodynamics predicts, correctly, that these energy sources will necessarily produce problems with entropy: some common names for this entropy are pollution, greenhouse gases, and global warming.
6. Nuclear Power. This is the direct conversion of mass to energy in accordance with the most famous equation in the world: E= mc2. Note that because the speed of light c is such a huge number, a nearly unimaginable amount of energy is available to us from small quantities of mass. Thus when we hear experts quacking about an energy crisis they are wrong. However, we do have an entropy crisis, and the Second Law of Thermodynamics assures us that nuclear power generation on Earth in wrong in principle: it treats the Earth as a closed system and necessarily will lead to problems in sustaining our ecosystem.
In this regard, the source of the Sun's energy is also nuclear. However, the Sun is some 150,000,000 km away from the Earth. So if we just think about the Earth, the energy streams through and we can "beat" the Second Law of Thermodynamics. Of course the total entropy of the Sun plus the Earth plus the rest of outer space is increasing.
 Finally, I mention an idea which seems to re-emerge every few years. Imagine we put a large array of solar panels on a satellite in stationary "geosynchrous" orbit above the Earth. We may then transmit the energy to the Earth's surface with microwaves.
Finally, I mention an idea which seems to re-emerge every few years. Imagine we put a large array of solar panels on a satellite in stationary "geosynchrous" orbit above the Earth. We may then transmit the energy to the Earth's surface with microwaves.
Perhaps technically feasible, this scheme keeps the Earth as an open system, and so at least in principle is correct.


