6.8: Forces Between Molecules
( \newcommand{\kernel}{\mathrm{null}\,}\)
We described in a qualitative manner in Section 6.3 the forces between molecules – the long-range attractive van der Waals forces caused by induced-dipole/induced-dipole interaction, and the shortrange repulsive Coulomb forces as the molecules approach each other closely, and how these intermolecular forces give rise to deviations from the “Boyle’s Law” expectations for the equation of state for an ideal gas. Presumably, if we knew the exact equation for the force law as a function of intermolecular distance, we could in principle calculate the equation of state; conversely, if we knew, through measurement, the form of the equation of state, we could deduce the form of the intermolecular forces. I have not actually done this myself; an early reference worthwhile to look up would be Lennard-Jones, Proc. Roy, Soc. A112, 214, (1926).
Qualitatively, the force law for the interaction between molecules would show a repulsive force rapidly falling off with distance when the molecules are very close (the molecules are “hard”) and a longer-range attractive force at larger distances. Two of the simpler equations that have been used to describe this are the Lennard-Jones potential:
V=D[1+(rcr)12−2(rcr)6]
and the Morse potential:
V=D(1−e−(r−re)/a)2
Each of these goes to V → D as r → ∞, and V = 0 when r = re. The Lennard-Jones potential (but not the Morse potential) goes to ∞ as r → 0.
These expressions cannot be “derived” in the usual sense; they are merely expressions that are useful for discussion in that they describe qualitatively the shape of the potential function that you would expect. The Lennard-Jones expression is often used in discussions of the van der Waals force: if the van der Waals attractive force is due mostly to induced-dipole/induced-dipole interaction, an r−6 term is about right. The Morse potential is used more often in discussion of the force between atoms in a bound molecule. If the Morse potential is put into the Schrödinger equation for an anharmonic oscillating diatomic molecule, it results in a simple solution for the eigenfunctions and eigenvalues, with the energy levels being given as quadratic (and no higher) in v+12.
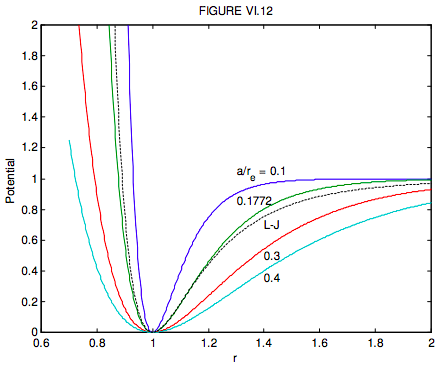
The parameter a in the Morse expression determines how narrow or how broad the minimum is. It is left as an exercise for the reader to show that the FWHm (full width at half minimum) of the Morse expression is the same as for the Lennard-Jones potential for
a=(2+√2)1/6−(2−√2)1/6ln(3+√8)=0.177212908
In figure VI.12, I show, as continuous curves, the Morse potentials (in order of increasing width) for a/re = 0.1, 0.1772, 0.3 and 0.4, and the Lennard-Jones potential as a dashed curve. Further comparisons between these two potential functions can be found in T.-C. Lim, Z. Naturforschung, 58a, 615, (2003).


