8.4: Reversible Adiabatic Expansion of an Ideal Gas

An adiabatic process is one in which no heat enters or leaves the system, and hence, for a reversible adiabatic process the first law takes the form dU = − PdV. But from equation 8.1.1, C_V = (∂U/∂T)_V. But the internal energy of an ideal gas depends only on the temperature and is independent of the volume (because there are no intermolecular forces), and so, for an ideal gas, C_V = dU/dT, and so we have dU = C_VdT. Thus for a reversible adiabatic process and an ideal gas, C_VdT = −PdV. (The minus sign shows that as V increases, T decreases, as expected.) But for a mole of an ideal gas, PV = RT = (C_P − C_V)T, or P = (C_P − C_V)T/V.

Therefore

\[ C_{v} d T=-\left(C_{P}-C_{V}\right) T d V / V\]

(You may be wondering whether C and V are molar, specific or total quantities. If you look at the equation you'll agree that it is valid whether the volume and heat capacities are molar, specific or total.)

Separate the variables and write γ for C_P/C_V:

\[ \frac{d T}{T}+(\gamma-1) \frac{d V}{V}=0.\]

Integrate:

\[ T V^{\gamma-1}=\text { constant }.\]

This shows how temperature and volume of an ideal gas vary during a reversible adiabatic expansion or compression. If the gas expands, the temperature goes down. If the gas is compressed, it becomes hot. Of course the pressure varies also, and the ideal gas conforms to the equation PV/T = constant. On elimination of T we obtain

\[ P V^{\gamma}=\text { constant }.\]

On elimination of V we obtain

\[ P^{-(\gamma-1)} T^{\gamma}=\text { constant. }\]

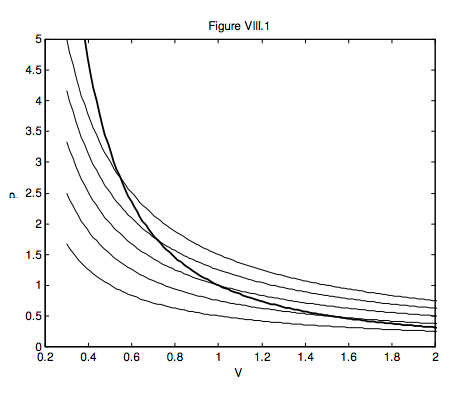
In figure VIII.1 I draw, as light curves, five isotherms – i.e. the paths that would be taken by an ideal gas in the PV plane in isothermal processes at five temperatures. I also show, as a heavier line, an adiabat, PV^γ = constant , which I calculated for γ = 5/3. The adiabat is steeper than the isotherms, and the curve shows that, as the gas expands adiabatically, the temperature drops. If you know the original temperature and the old and new volumes, equation 8.4.3 will enable you to calculate the new temperature. If you know the original temperature and the old and new pressures, equation 8.4.5 will enable you to calculate the new temperature. While these purely thermodynamic arguments show that a gas becomes hotter if you compress it, this is also to be expected at the microscopic level. Thus, if a molecule bounces elastically against a piston that is moving towards it, it will gain kinetic energy, and it will lose kinetic energy if it bounces off a piston that is moving away from it.

Let us calculate the work done by a mole of an ideal gas in a reversible adiabatic expansion from (P₁ , V₁) to (P₂ , V₂):

\[ W=\int_{V_{1}}^{V_{2}} P d V.\]

For a reversible adiabatic expansion, PV^γ = K, and therefore

\[ W=K \int_{v_{1}}^{v_{2}} V^{-\gamma} d V=\frac{K}{\gamma-1}\left(V_{1}^{-(\gamma-1)}-V_{2}^{-(\gamma-1)}\right)\]

That is,

\[ W=\frac{P_{1} V_{1}-P_{2} V_{2}}{\gamma-1}=\frac{R\left(T_{1}-T_{2}\right)}{\gamma-1}\]

(Note that T₂ < T₁ in this adiabatic expansion.)

Compare this with equation 8.3.1 for an isothermal expansion.

Note also that, since R = C_P − C_V and C_P/C_V = γ this can also be written

\[ W=C_{V}\left(T_{1}-T_{2}\right)\]

This is also equal to the heat that would be lost if the gas were to cool from T1 to T2 at constant volume. Think about this! Is it coincidence, or must it be so?

Here is a useful exercise. In figure VIII.2, a gas goes from (P₁, V₁) to (P₂, V₂) via three different reversible routes:

(a) An isobaric expansion followed by an isochoric decrease in pressure;

(b) An isochoric decrease in pressure followed by an isobaric expansion;

(c) An adiabatic expansion.

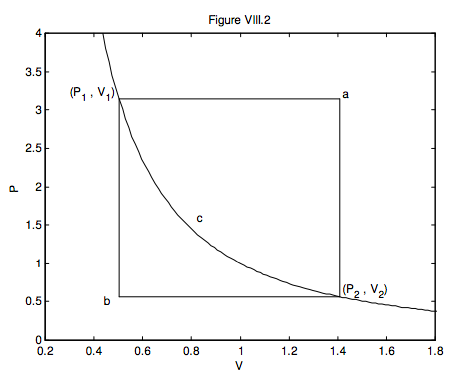
At each stage, calculate the work done on or by the gas, the heat gained by the gas or lost from the gas, and the increase or decrease of the internal energy of the gas. This exercise will illustrate that U is a function of state, but Q and W are not. (I expect the answers to be in algebra; ignore the numbers on the axes – they don’t mean anything in particular.)